Stock Prices

In physics it takes three laws to explain 99% of the data; in finance it takes more than 99 laws to explain about 3% - Andrew Lo

Stock price data encompasses historical prices as well as corporate actions such as stock splits, dividends, and delistings. The CRSP database is a standard resource in academic research due to its comprehensive coverage of both active and delisted stocks, which supports unbiased and representative analysis. Efficient storage, retrieval, and processing of such structured financial data are enabled by tools such as SQL, SQLAlchemy, Redis, and Pandas. We examine statistical moments, assume log-normal distributions, and explore alternative correlation measures for modeling stock return behavior and dependencies.

# By: Terence Lim, 2020-2025 (terence-lim.github.io)
import numpy as np
import scipy
import pandas as pd
from pandas import DataFrame, Series
import matplotlib.pyplot as plt
import warnings
from tqdm import tqdm
from finds.database import SQL, RedisDB
from finds.structured import BusDay, CRSP, CRSPBuffer, Benchmarks
from finds.utils import Finder
from secret import credentials, CRSP_DATE, paths
VERBOSE = 0

# %matplotlib qt

FinDS package

Developed over a journey to support financial data science workflows, our FinDS Python package integrates:

• Use of database engines like SQL, Redis, and MongoDB to manage large structured and unstructured datasets

• Tools for accessing key financial datasets, including CRSP, Compustat, IBES, and TAQ

• Interfaces to public data sources such as FRED, SEC EDGAR, and the BEA

• Utilities for extracting data from academic and research websites

• Recipes for applying a range of statistical and machine learning methods, including network graphs, natural language processing and large language models.

SQL

Structured Query Language (SQL) is a popular tool for storing and managing relational data organized into tables with columns (fields) and rows (records). Open-source systems like MySQL are widely used to implement relational databases, and Python libraries such as SQLAlchemy provide convenient interfaces for interacting with them. Additionally, the Pandas library allows users to run SQL queries and load the results directly into DataFrames for efficient analysis.

Redis

Redis is an open-source, in-memory data store commonly used as a caching layer. It helps improve performance by storing frequently accessed data in memory, thereby reducing the load on slower, primary databases.

# open database connections
sql = SQL(**credentials['sql'], verbose=VERBOSE)
rdb = RedisDB(**credentials['redis'])
bd = BusDay(sql, endweek=3, verbose=VERBOSE)
crsp = CRSP(sql, bd, rdb=rdb, verbose=VERBOSE)
bench = Benchmarks(sql, bd, verbose=VERBOSE)
find = Finder(sql)
outdir = paths['scratch']

Stock price data

Besides the historical prices of stocks, their adjustments such as identifier changes, stock splits, dividends, mergers, and delistings must also be recorded to accurately analyze performance over time.

CRSP stocks

The Center for Research in Security Prices (CRSP) provides the most widely used data for academic research into US stocks. It includes both successful and unsuccessful entities, rather than just those that have “survived” over time. This helps avoid the pitfalls of focusing only on surviving entities which can lead to an overestimation of average performance and underestimation of risk. It also captures corporate actions by standardizing data on events such as name changes, distributions and delistings. This information is recorded and validated from official sources, integrated into its historical databases along with details like announcement and effective dates, adjustment factors, and impact on stock performance calculations.

# describe the database schema of the CRP Stocks `names` table 
DataFrame(**sql.run('describe names'))

	Field	Type	Null	Key	Default	Extra
0	date	int	NO	PRI	None
1	comnam	varchar(32)	YES		None
2	ncusip	varchar(8)	YES	MUL	None
3	shrcls	varchar(1)	YES		None
4	ticker	varchar(5)	YES		None
5	permno	int	NO	PRI	None
6	nameendt	int	YES		None
7	shrcd	smallint	YES		None
8	exchcd	smallint	YES		None
9	siccd	smallint	YES		None
10	tsymbol	varchar(7)	YES		None
11	naics	int	YES		None
12	primexch	varchar(1)	YES		None
13	trdstat	varchar(1)	YES		None
14	secstat	varchar(4)	YES		None
15	permco	int	YES		None

SQL select and join statements to retrieve Apple Computer’s identifiers and corporate actions, such as stock splits and dividends. Commonly used SQL commands listed at the end of this notebook.

# double up the % when passing sql command stringo to pandas
names_df = pd.read_sql("select * from names where comnam like '%%APPLE COMPUTER%%'", con=sql.engine)
names_df

	date	comnam	ncusip	shrcls	ticker	permno	nameendt	shrcd	exchcd	siccd	tsymbol	naics	primexch	trdstat	secstat	permco
0	19801212	APPLE COMPUTER INC	03783310		AAPL	14593	19821031	11	3	3573		0	Q	A	R	7
1	19821101	APPLE COMPUTER INC	03783310		AAPL	14593	20040609	11	3	3573	AAPL	0	Q	A	R	7
2	20040610	APPLE COMPUTER INC	03783310		AAPL	14593	20070110	11	3	3573	AAPL	334111	Q	A	R	7

# inner join of identifiers (names) and distributions (dist) tables
cmd = """
select distinct names.permno, divamt, facpr, exdt, comnam, ticker from names 
inner join dist
on names.permno = dist.permno
where names.comnam like '%%APPLE COMPUTER%%'
"""
dist_df = pd.read_sql(cmd, con=sql.engine)
dist_df

	permno	divamt	facpr	exdt	comnam	ticker
0	14593	0.12	0.0	19870511	APPLE COMPUTER INC	AAPL
1	14593	0.06	0.0	19870810	APPLE COMPUTER INC	AAPL
2	14593	0.08	0.0	19871117	APPLE COMPUTER INC	AAPL
3	14593	0.08	0.0	19880212	APPLE COMPUTER INC	AAPL
4	14593	0.08	0.0	19880516	APPLE COMPUTER INC	AAPL
...	...	...	...	...	...	...
86	14593	0.00	1.0	19870616	APPLE COMPUTER INC	AAPL
87	14593	0.00	1.0	20000621	APPLE COMPUTER INC	AAPL
88	14593	0.00	1.0	20050228	APPLE COMPUTER INC	AAPL
89	14593	0.00	6.0	20140609	APPLE COMPUTER INC	AAPL
90	14593	0.00	3.0	20200831	APPLE COMPUTER INC	AAPL

91 rows × 6 columns

Stock splits and dividends

An investor’s total holding returns (ret in CRSP) include gains from appreciated stock prices (prc), adjusted for stock splits (facpr), plus ordinary cash dividends (divamt). Specifically, on ex-dates \(t\):

\[ret_t = \dfrac{prc_t \ (1 + facpr_t) + div_t}{prc_{t-1}}\]

The Factor to Adjust Price (facpr) values over time can be used to adjust prices for distributions such as stock dividends and splits so that stock prices before and after one or more distributions are comparable. Historical cumulative adjust factors are computed by additing 1 to and then taking cumulative product from current to earlier time periods. This cumulative factor between two dates is divided into the earlier raw stock price to derive comparable split-adjusted prices. Hence to split-adjust CRSP raw prices

• apply cumulative factor to raw prices before corresponding ex-date

• back-fill to dates prior to ex-date

• default factor after latest ex-date is 1

yfinance

The yfinance Python library enables users to access current financial data from Yahoo Finance.

import yfinance as yf
ticker = yf.Ticker('AAPL')
df = ticker.history(period='max')
df[df['Dividends'].gt(0) | df['Stock Splits'].ne(0)]

	Open	High	Low	Close	Volume	Dividends	Stock Splits
Date
1987-05-11 00:00:00-04:00	0.264817	0.273415	0.263957	0.264817	197276800	0.000536	0.0
1987-06-16 00:00:00-04:00	0.285452	0.287171	0.261378	0.285452	342720000	0.000000	2.0
1987-08-10 00:00:00-04:00	0.332310	0.332310	0.315091	0.332310	77996800	0.000536	0.0
1987-11-17 00:00:00-05:00	0.253658	0.255384	0.241579	0.241579	268800000	0.000714	0.0
1988-02-12 00:00:00-05:00	0.280957	0.287009	0.280093	0.283551	137760000	0.000714	0.0
...	...	...	...	...	...	...	...
2024-02-09 00:00:00-05:00	187.763406	189.097120	187.116467	187.962479	45155200	0.240000	0.0
2024-05-10 00:00:00-04:00	184.280653	184.470019	181.519943	182.436859	50759500	0.250000	0.0
2024-08-12 00:00:00-04:00	215.595507	219.027939	215.126538	217.052292	38028100	0.250000	0.0
2024-11-08 00:00:00-05:00	226.920500	228.408869	226.161340	226.710739	38328800	0.250000	0.0
2025-02-10 00:00:00-05:00	229.570007	230.589996	227.199997	227.649994	33115600	0.250000	0.0

91 rows × 7 columns

The daily Close prices from yFinance have been adjusted for stock splits and dividend payments. As a result, the plotted values directly represent cumulative total holding returns.

df['Close'].div(df['Close'].iloc[0]).plot(title="APPL close prices from yfinance")

<Axes: title={'center': 'APPL close prices from yfinance'}, xlabel='Date'>

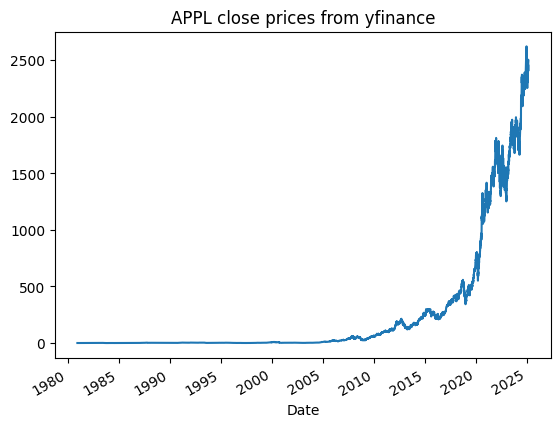
To retrieve unadjusted historical prices accounting for stock splits and dividends, first apply the split factors to determine the original dividends per unadjusted share. The resulting values closely match the CRSP divamt figures, with minor differences likely due to cumulative numerical precision errors.

split = df['Stock Splits'].where(df['Stock Splits'] != 0.0, 1)\
    .shift(-1).fillna(1).iloc[::-1].cumprod().iloc[::-1]       # cumulate the split factors back in time
df['unadj_div'] = df['Dividends'] * split.shift(1).fillna(split.iloc[0])   # apply the split factors to dividends
df.set_index(df.index.strftime('%Y-%m-%d'))[(df['unadj_div'] > 0).values]

	Open	High	Low	Close	Volume	Dividends	Stock Splits	unadj_div
Date
1987-05-11	0.264817	0.273415	0.263957	0.264817	197276800	0.000536	0.0	0.120064
1987-08-10	0.332310	0.332310	0.315091	0.332310	77996800	0.000536	0.0	0.060032
1987-11-17	0.253658	0.255384	0.241579	0.241579	268800000	0.000714	0.0	0.079968
1988-02-12	0.280957	0.287009	0.280093	0.283551	137760000	0.000714	0.0	0.079968
1988-05-16	0.280647	0.286711	0.277183	0.285845	74760000	0.000714	0.0	0.079968
...	...	...	...	...	...	...	...	...
2024-02-09	187.763406	189.097120	187.116467	187.962479	45155200	0.240000	0.0	0.240000
2024-05-10	184.280653	184.470019	181.519943	182.436859	50759500	0.250000	0.0	0.250000
2024-08-12	215.595507	219.027939	215.126538	217.052292	38028100	0.250000	0.0	0.250000
2024-11-08	226.920500	228.408869	226.161340	226.710739	38328800	0.250000	0.0	0.250000
2025-02-10	229.570007	230.589996	227.199997	227.649994	33115600	0.250000	0.0	0.250000

86 rows × 8 columns

Next, we work backward through time to reconstruct the original stock prices using daily holding returns and closing prices. Stock splits and dividends are accounted for on ex-dates by applying the rearranged formula:

\[prc_{t-1} = \dfrac{(1+facpr_t) (prc_t + div_t)}{ret_t}\]

rets = df['Close'] / df['Close'].shift(1)
prc = df['Close'].iloc[-1]
div = 0
fac = 0
ret = 1
for i, t in enumerate(df.index[::-1]):     # iterate over days in reverse
    df.loc[t, 'unadj_prc'] =  (((fac if fac else 1) * prc) + div) / ret
    prc = df.loc[t, 'unadj_prc']
    div = df.loc[t, 'unadj_div']
    fac = df.loc[t, 'Stock Splits']
    ret = rets.loc[t]
df.set_index(df.index.strftime('%Y-%m-%d'))

	Open	High	Low	Close	Volume	Dividends	Stock Splits	unadj_div	unadj_prc
Date
1980-12-12	0.098726	0.099155	0.098726	0.098726	469033600	0.0	0.0	0.0	28.757305
1980-12-15	0.094005	0.094005	0.093575	0.093575	175884800	0.0	0.0	0.0	27.257003
1980-12-16	0.087136	0.087136	0.086707	0.086707	105728000	0.0	0.0	0.0	25.256412
1980-12-17	0.088853	0.089282	0.088853	0.088853	86441600	0.0	0.0	0.0	25.881523
1980-12-18	0.091429	0.091858	0.091429	0.091429	73449600	0.0	0.0	0.0	26.631895
...	...	...	...	...	...	...	...	...	...
2025-02-24	244.929993	248.860001	244.419998	247.100006	51326400	0.0	0.0	0.0	247.100006
2025-02-25	248.000000	250.000000	244.910004	247.039993	48013300	0.0	0.0	0.0	247.039993
2025-02-26	244.330002	244.979996	239.130005	240.360001	44433600	0.0	0.0	0.0	240.360001
2025-02-27	239.410004	242.460007	237.059998	237.300003	41153600	0.0	0.0	0.0	237.300003
2025-02-28	236.949997	242.089996	230.199997	241.839996	56796200	0.0	0.0	0.0	241.839996

11144 rows × 9 columns

The unadjusted price computer and the original closing prices from CRSP during the early days of AAPL stock are nearly identical, with only small differences due to cumulative numerical precision errors.

price_df = pd.read_sql(f"select permno, date, abs(prc) from daily where permno={names_df['permno'][0]}", con=sql.engine)
price_df.head(10)

	permno	date	abs(prc)
0	14593	19801212	28.8125
1	14593	19801215	27.3125
2	14593	19801216	25.3125
3	14593	19801217	25.9375
4	14593	19801218	26.6875
5	14593	19801219	28.3125
6	14593	19801222	29.6875
7	14593	19801223	30.9375
8	14593	19801224	32.5625
9	14593	19801226	35.5625

Market capitalization

Following Fama and French (1992), academic research typically focuses on U.S.-domiciled stocks, specifically those with a share code (shrcd) of 10 or 11, that are listed on major exchanges (exchange code (exchcd) of 1, 2, or 3).

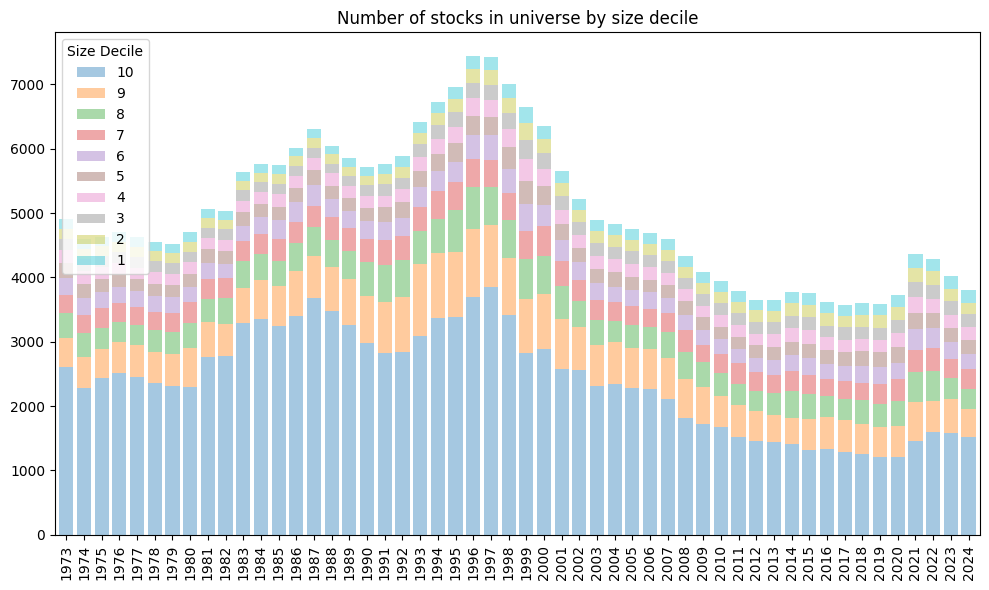
Stocks are often sorted into ten deciles based on market capitalization, with the smallest stocks placed in the 10th decile. These decile breakpoints are determined using only NYSE-listed stocks. For companies with multiple classes of securities, total market value is calculated by summing the market capitalization of all classes. Since CRSP reports shares outstanding (shrout) in thousands, all market capitalization values must be multiplied by 1,000 to reflect their actual size.

Plot the number of stocks in and the market cap breakpoints of each size decile by year:

# retrieve universe of stocks annually from 1981
start = bd.endyr(19731231)
rebals = bd.date_range(start, CRSP_DATE, freq=12)
univs = {rebal: crsp.get_universe(date=rebal) for rebal in rebals}
num = dict()
for date, univ in univs.items():
    num[str(date//10000)] = {decile: sum(univ['decile']==decile)
                             for decile in range(10, 0, -1)}
num = DataFrame.from_dict(num, orient='index')

# plot number of stocks in each size decile
fig, ax = plt.subplots(figsize=(10, 6))
ax.set_title('Number of stocks in universe by size decile')
num.plot.bar(stacked=True, ax=ax, width=.8, alpha=0.4)
#set_xtickbins(ax=ax, nbins=len(cap)//10)
plt.legend(title='Size Decile', loc='upper left')
plt.tight_layout()

# If a company has multiple share classes, sum up its total market capitalization 
# instead of separate capital values for each share class
names = find('ALPHABET', 'comnam').groupby('permno').tail(1).set_index('permno')
names

	date	comnam	ncusip	shrcls	ticker	nameendt	shrcd	exchcd	siccd	tsymbol	naics	primexch	trdstat	secstat	permco
permno
14542	20231013	ALPHABET INC	02079K10	C	GOOG	20241231	11	3	7375	GOOG	541511	Q	A	R	45483
90319	20231013	ALPHABET INC	02079K30	A	GOOGL	20241231	11	3	7375	GOOGL	541511	Q	A	R	45483

univ.loc[names.index]  # market caps of share class (cap) and total company (capco)

	cap	capco	decile	nyse	siccd	prc	naics
permno
14542	1.053895e+09	2.159975e+09	1	False	7375	190.44	541511
90319	1.106080e+09	2.159975e+09	1	False	7375	189.30	541511

Stock delistings

An important feature of the CRSP database is that it is free of survivorship-bias. It includes the historical records of stocks that have delisted from trading on the exchanges.

In CRSP Monthly, the Delisting Return is calculated from the last month ending price to the last daily trading price if no other delisting information is available. In this case the delisting payment date is the same as the delisting date. If the return is calculated from a daily price, it is a partial-month return. The partial-month returns are not truly Delisting Returns since they do not represent values after delisting, but allow the researcher to make a more accurate estimate of the Delisting Returns.

Following Bali, Engle, and Murray (2016) and Shumway (1997): we can construct returns adjusted for delistings, which result when a company is acquired, ceases operations, or fails to meet exchange listing requirements. The adjustment reflects the partial month of returns to investors who bought the stock in the month before the delisting. For certain delisting codes ([500, 520, 551..574, 580, 584]) where the delisting return is missing, a delisting return of -30% is assumed which reflects the average recovery amount after delisting.

# Show sample of original CRSP Monthly ret and dlret before and after adjustment            
pd.read_sql('select * from monthly where dlstcd>100 and date=20041130', sql.engine)\
  .set_index('permno')\
  .rename(columns={'ret': 'original_ret'})\
  .join(crsp.get_ret(beg=20041101, end=20041130), how='left')\
  .round(4)

	date	prc	original_ret	retx	dlstcd	dlret	ret
permno
10275	20041130	NaN	NaN	NaN	584	-0.2703	-0.2703
10418	20041130	NaN	NaN	NaN	520	0.0509	0.0509
11194	20041130	NaN	NaN	NaN	233	0.0066	0.0066
12010	20041130	NaN	NaN	NaN	587	0.0490	0.0490
20459	20041130	NaN	NaN	NaN	231	0.0724	0.0724
32897	20041130	NaN	NaN	NaN	584	-0.2357	-0.2357
55589	20041130	NaN	NaN	NaN	233	-0.0114	-0.0114
64290	20041130	13.70	0.0178	0.0178	233	0.0000	0.0178
67708	20041130	NaN	NaN	NaN	233	0.0164	0.0164
69593	20041130	NaN	NaN	NaN	331	0.0998	0.0998
69681	20041130	NaN	NaN	NaN	584	-0.4853	-0.4853
70447	20041130	5.80	-0.2246	-0.2246	570	NaN	-0.4572
75606	20041130	NaN	NaN	NaN	520	-0.2466	-0.2466
75684	20041130	NaN	NaN	NaN	233	0.0094	0.0094
76306	20041130	NaN	NaN	NaN	241	-0.0329	-0.0329
76691	20041130	NaN	NaN	NaN	582	0.0127	0.0127
77838	20041130	NaN	NaN	NaN	520	-0.0041	-0.0041
79149	20041130	NaN	NaN	NaN	574	-0.2088	-0.2088
79523	20041130	NaN	NaN	NaN	233	0.0043	0.0043
80211	20041130	NaN	NaN	NaN	470	0.0186	0.0186
80714	20041130	NaN	NaN	NaN	332	0.0337	0.0337
82491	20041130	4.21	-0.0644	-0.0644	551	0.0689	0.0000
83583	20041130	125.10	0.2810	0.2810	241	0.0624	0.3608
83702	20041130	NaN	NaN	NaN	587	0.2667	0.2667
83995	20041130	26.58	0.2374	0.2374	231	0.0394	0.2861
84047	20041130	16.35	0.0467	0.0467	241	-0.2661	-0.2318
86123	20041130	NaN	NaN	NaN	233	0.0059	0.0059
86307	20041130	NaN	NaN	NaN	233	0.0223	0.0223
86388	20041130	NaN	NaN	NaN	584	-0.0337	-0.0337
86991	20041130	NaN	NaN	NaN	233	0.0106	0.0106
87126	20041130	NaN	NaN	NaN	231	0.0784	0.0784
87158	20041130	NaN	NaN	NaN	233	0.0086	0.0086
87247	20041130	NaN	NaN	NaN	233	0.0046	0.0046
88670	20041130	NaN	NaN	NaN	470	0.0013	0.0013
89186	20041130	NaN	NaN	NaN	331	0.0696	0.0696
89385	20041130	NaN	NaN	NaN	231	0.2959	0.2959
89936	20041130	NaN	NaN	NaN	231	0.0719	0.0719
89939	20041130	NaN	NaN	NaN	233	0.0059	0.0059

Properties of stock returns

Long-run market averages

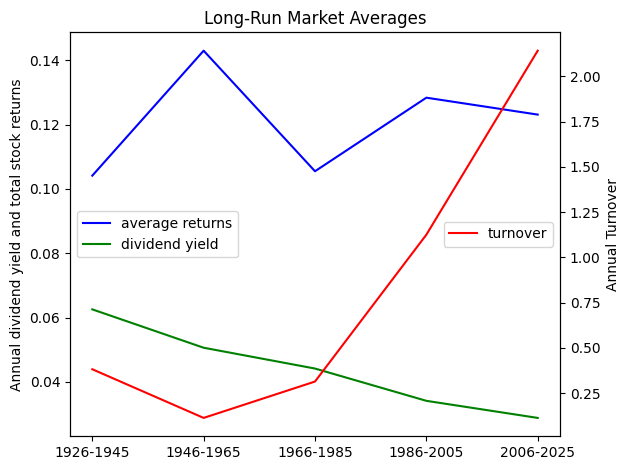
Calculate and plot the time series of annual cross-sectional averages of stock returns, where each year’s average is cap-weighted, and the final time series is equal-weighted.

Over time, the contribution of dividend yield to total average stock returns has decreased, while share trading turnover has increased.

# Loop over the 20-year eras, and compute means of annual cap-weighted averages
years = range(1925, 2025, 20)
results = DataFrame(columns=['divyld', 'turnover', 'means'])
for era in tqdm(years):
    label = f"{era+1}-{era+20}"
    divyld, means, turnover = {}, {}, {}

    for year in bd.date_range(era, min(CRSP_DATE//10000 -1 , era+19), freq=12):
        # universe stocks at end of year
        univ = crsp.get_universe(bd.endyr(year))

        # retrieve cap-weighted average of next year's returns
        cmd = f"""
select permno, SUM(LOG(1+ret)) AS ret FROM daily
WHERE date > {bd.endyr(year)} AND date <= {bd.endyr(year, 1)}
GROUP BY permno
""".strip()
        data = pd.read_sql(cmd, sql.engine)
        df = data.set_index('permno').join(univ['cap'], how='right').dropna()
        means[year] = (np.exp(df['ret'])-1).dot(df['cap']) / df['cap'].sum()

        # retrieve cap-weighted average of annualized turnover
        cmd = f"""
select permno, 252*AVG(vol/(shrout*1000)) AS turnover FROM daily
WHERE date > {bd.endyr(year)} AND date <= {bd.endyr(year, 1)}
GROUP BY permno
""".strip()
        data = pd.read_sql(cmd, sql.engine)
        df = data.set_index('permno').join(univ['cap'], how='right').dropna()
        turnover[year] = df['turnover'].dot(df['cap']) / df['cap'].sum()

        # retrieve cap-weighted average of annual dividend amounts
        cmd = f"""
SELECT dist.permno as permno, SUM(daily.shrout * dist.divamt) AS divamt
FROM dist INNER JOIN daily
ON daily.permno = dist.permno AND daily.date = dist.exdt
WHERE dist.divamt > 0 AND dist.exdt > {bd.endyr(year)} 
  AND dist.exdt <= {bd.endyr(year, 1)}
GROUP BY permno
""".strip()
        data = pd.read_sql(cmd, sql.engine)
        df = data.set_index('permno').join(univ['cap'], how='right').dropna()
        divyld[year] = df['divamt'].sum() / df['cap'].sum()

    results.loc[label, 'turnover'] = np.mean(list(turnover.values()))
    results.loc[label, 'divyld'] = np.mean(list(divyld.values()))
    results.loc[label, 'means'] = np.mean(list(means.values()))

100%|██████████| 5/5 [1:03:37<00:00, 763.46s/it]

# Plot mean returns, dividend yield and turnover using both y-axes
fig, ax = plt.subplots()
ax.plot(results['means'], color="blue")
ax.plot(results['divyld'], color="green")
ax.legend(['average returns', 'dividend yield'], loc="center left")
ax.set_ylabel("Annual dividend yield and total stock returns")
bx = ax.twinx()
bx.plot(results['turnover'], color="red")
bx.set_ylabel("Annual Turnover")
bx.legend(['turnover'], loc="center right")
plt.title("Long-Run Market Averages")
plt.tight_layout()

Statistical moments

The volatility of an asset is usually measured using the standard deviation of the returns. The common practice is to report the annualized volatility using the square-root rule which assumes that variance scales linearly with time: e.g. daily by \(\sqrt{252}\), weekly by \(\sqrt{52}\), monthly by \(\sqrt{12}\). Mean returns are annualized by multiplying by the respective number of periods in a year.

A normal distribution is symmetric and thin-tailed, and so has no skewness or excess kurtosis. However, many return series are both skewed and fat-tailed (kurtosis in excess of 3). A left-skewed distribution is longer on the left side of its peak than on its right. In other words, a left-skewed distribution has a long tail on its left side, where the mean typically lies to the left of its median. Left skew is also referred to as negative skew. Right or positive skew has the opposite properties.

Stock prices are often modeled with a log-normal distribution because prices cannot be negative. Large positive jumps are possible, but extreme negative moves are bounded at zero, hence the distribution of log-normal returns is positively-skewed with a long right tail. The skewness of a log-normal distribution is given by: \((e^{\sigma^2} + 2) \sqrt{e^{\sigma^2} - 1}\)

By Jensen’s inequality, the arithmetic mean is greater than the geometric mean. Under the assumption of log-normality, the amount by which the arithmetic mean exceeds the geometric means of returns is half the volatility.

• Suppose the continuously compounded (log) returns ( r_t ) are normally distributed with mean ( \mu ) and variance ( \sigma^2 ): \(r_t = \ln \left(\frac{P_t}{P_{t-1}}\right) \sim N(\mu, \sigma^2)\)

• The geometric mean return is given by \(\mu_G = \frac{1}{T} \sum_{t=1}^{T} r_t\), with expectation \(\mathbb{E}[r_t] = \mu\)

• The arithmetic mean of the simple returns is approximately given by \(\mu_A \approx e^{\mu + \frac{1}{2} \sigma^2} - 1 \approx \mu_G + \frac{1}{2} \sigma^2\), using the first-order approximation \(e^x \approx 1 + x\) for small \(x\).

Jarque-Bera test

The Jarque-Bera test statistic can be used to test whether the sample skewness and kurtosis are compatible with an assumption that the returns are normally distributed. When returns are normally distributed, the skewness is asymptotically normally distributed with a variance of 6, so (skewness)\(^2/6\) has a \(\chi^2_1\) distribution. Meanwhile, the kurtosis is asymptotically normally distributed with mean 3 and variance of 24, and so (kurtosis - 3)\(^2/24\) also has a \(\chi^2_1\) distribution. These two statistics are asymptotically independent (uncorrelated), and so their sum is \(~\chi^2_2\)

# Compute the stock returns sampled at various frequencies
intervals = {'annual': (12, 1), 'monthly': ('e', 12), 'weekly': ('w', 52), 'daily': ('d', 252)}
moments = []
begdate, enddate = bd.begyr(CRSP_DATE//10000 - 19), bd.endyr(CRSP_DATE//10000)

for dataset, (freq, annualize) in intervals.items():

    # If annual or monthly frequency, use StocksBuffer to pre-load all monthly returns
    if dataset not in ['daily', 'weekly']:
        stocks = CRSPBuffer(stocks=crsp, dataset='monthly', fields=['ret'],
                            beg=bd.begyr(begdate), end=enddate)
    if dataset in ['weekly']:  # weekly returns already computed from CRSP Daily, and cached
        stocks = crsp

    univ_year = bd.endyr(begdate - 1)  # universe as of end of previous calendar year               
    dates = bd.date_range(bd.endyr(begdate), bd.endyr(enddate), freq=freq)
    allstocks = []
    for beg, end in tqdm(bd.date_tuples(dates)):

        # Update the investment universe every calendar year                                        
        if bd.endyr(beg) != univ_year:
            univ = crsp.get_universe(univ_year)
            univ_year = bd.endyr(beg)

            # Use StocksBuffer to cache daily returns for the new calendar year                     
            if dataset in ['daily']:
                stocks = CRSPBuffer(stocks=crsp, dataset='daily', fields=['ret'],
                                    beg=bd.offset(beg, -1), end=bd.endyr(end))

        # retrieve returns for universe stocks                                                      
        ret = stocks.get_ret(beg=beg, end=end).reindex(univ.index)
        allstocks.append(ret.rename(end))

    # combine all years' stock returns, require stock in all years                                  
    allstocks = pd.concat(allstocks, axis=1, join='inner')

    # compute annualized moments, ignoring small sample warnings
    with warnings.catch_warnings():
        warnings.simplefilter("ignore")
        out = {
            f"MeanAnnualized": np.nanmedian(
                np.nanmean(np.log(1 + allstocks), axis=1)) * annualize,
            f"VolAnnualized": np.nanmedian(
                np.nanstd(allstocks, axis=1, ddof=0)) * np.sqrt(annualize),
            f"Skewness": np.nanmedian(
                scipy.stats.skew(allstocks, nan_policy='omit', axis=1)),
            f"ExcessKurtosis": np.nanmedian(
                scipy.stats.kurtosis(allstocks, nan_policy='omit', axis=1)),
            f"Count": len(allstocks),
        }
    df = DataFrame({dataset: Series(out)}).T
    moments.append(df)
moments = pd.concat(moments, axis=0)  # accumulate df to results                                    
moments.reset_index().to_json(outdir / 'moments.json')

100%|██████████| 19/19 [00:00<00:00, 37.61it/s]
100%|██████████| 228/228 [00:04<00:00, 53.61it/s]
100%|██████████| 991/991 [00:01<00:00, 517.26it/s]
100%|██████████| 4781/4781 [07:05<00:00, 11.23it/s] 

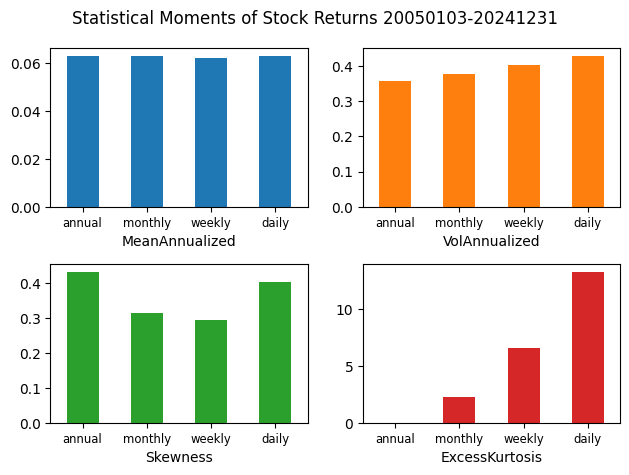
As we move from annual to daily sampling, stock returns exhibit greater kurtosis (i.e. fat tails) and annualized standard deviation. Skewness is positive – the right tail of the distribution is longer than the left tail – but are U-shaped with daily and annual returns featuring more positive-skewness than weekly or monthly.

moments

	MeanAnnualized	VolAnnualized	Skewness	ExcessKurtosis	Count
annual	0.063249	0.356397	0.434219	0.002332	1519.0
monthly	0.063249	0.376568	0.314758	2.242009	1519.0
weekly	0.062119	0.402871	0.293850	6.612277	1519.0
daily	0.063325	0.429472	0.404691	13.332600	1519.0

fig, axes = plt.subplots(2,2)
for ix, ax in enumerate(axes.flatten()):
    moments[moments.columns[ix]].plot.bar(ax=ax, color=f"C{ix}")
    ax.set_xticklabels(moments.index, rotation=0, fontsize='small')
    ax.set_xlabel(moments.columns[ix])
plt.suptitle(f"Statistical Moments of Stock Returns {begdate}-{enddate}")
plt.tight_layout()
plt.show()

Correlations

Pearson’s correlation, also known as the linear correlation estimator, measures the strength of a linear relationship between two variables. However, alternative methods can better capture nonlinear dependencies:

• Spearman’s rank correlation applies Pearson’s correlation to the ranked values of observations, measuring monotonic relationships while being less sensitive to outliers.

• Kendall’s \(\tau\) quantifies the relationship between two variables by comparing the number of concordant and discordant pairs – pairs that agree or disagree on ordering. It is robust to outliers and effective for skewed or non-normally distributed data.

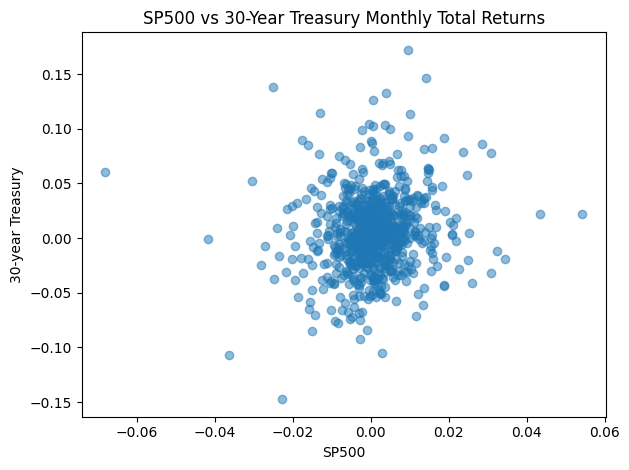
Monthly SP500 and 30-year Treasury total market returns show positive correlation, which is fairly robust across the three methods.

# retrieve SP500 and 30-Year Treasury total market returns from CRSP Indexes
ret = bench.get_series(['sprtrn', 'b30ret(mo)'], field='ret').dropna()
ret

permno	sprtrn	b30ret(mo)
date
19620731	0.006917	-0.008187
19620831	0.007498	0.031939
19620928	0.008965	0.015465
19621031	-0.000354	0.012171
19621130	-0.002403	0.003414
...	...	...
20240830	0.010093	0.020778
20240930	0.004237	0.015521
20241031	-0.018615	-0.053895
20241129	0.005608	0.021467
20241231	-0.004285	-0.063115

749 rows × 2 columns

# Compute alternative measures of correlation
DataFrame(dict(spearman=scipy.stats.spearmanr(ret['sprtrn'], ret['b30ret(mo)'])[0],
               kendall=scipy.stats.kendalltau(ret['sprtrn'], ret['b30ret(mo)'])[0],
               pearson=scipy.stats.pearsonr(ret['sprtrn'], ret['b30ret(mo)'])[0]),
               index=['Correlation of SP500 vs 30-Year Treasury Total Returns']).round(4)

	spearman	kendall	pearson
Correlation of SP500 vs 30-Year Treasury Total Returns	0.1348	0.0933	0.1275

# Scatter plot of SP500 and and 30-year Treasury total market returns
fig, ax = plt.subplots()
ax.scatter(ret['sprtrn'], ret['b30ret(mo)'], alpha=0.5)
ax.set_xlabel('SP500')
ax.set_ylabel('30-year Treasury')
plt.title('SP500 vs 30-Year Treasury Monthly Total Returns')
plt.tight_layout()            

APPENDIX

SQL commands

• Manage tables

  • CREATE DATABASE – Creates a new database.

  • CREATE TABLE – Creates a new table.

  • DELETE – Delete data from a table.

  • DROP COLUMN – Deletes a column from a table.

  • DROP DATABASE – Deletes the entire database.

  • DROP TABLE – Deletes a table from a database.

  • TRUNCATE TABLE – Deletes the data but does not delete the table.

• Querying a table

  • SELECT – Used to select data from a database, which is then returned in a results set.

  • SELECT DISTINCT – Sames as SELECT, except duplicate values are excluded.

  • SELECT INTO – Copies data from one table and inserts it into another.

  • UNIQUE – This constraint ensures all values in a column are unique.

  • FROM – Specifies which table to select or delete data from.

  • AS – Renames a table or column with an alias value which only exists for the duration of the query.

• Query conditions

  • WHERE – Filters results to only include data which meets the given condition.

  • AND – Used to join separate conditions within a WHERE clause.

  • BETWEEN – Selects values within the given range.

  • IS NULL – Tests for empty (NULL) values.

  • IS NOT NULL – The reverse of NULL. Tests for values that aren’t empty / NULL.

  • LIKE – Returns true if the operand value matches a pattern.

  • NOT – Returns true if a record DOESN’T meet the condition.

  • OR – Used alongside WHERE to include data when either condition is true.

• Organize results

  • ORDER BY – Used to sort the result data in ascending (default) or descending order through the use of ASC or DESC keywords.

  • GROUP BY – Used alongside aggregate functions (COUNT, MAX, MIN, SUM, AVG) to group the results.

• Join tables

  • INNER JOIN returns rows that have matching values in both tables.

  • LEFT JOIN returns all rows from the left table, and the matching rows from the right table.-

  • RIGHT JOIN returns all rows from the right table, and the matching records from the left table

  • FULL OUTER JOIN returns all rows when there is a match in either left table or right table.

References:

Fama, Eugene F., and Kenneth R. French. 1992. “The cross-section of expected stock returns.” The Journal of Finance 47 (2): 427–65.

Shumway, Tyler. 1997. The Delisting Bias in CRSP Data. The Journal of Finance, 52, 327-340.

Bali, Turan G, Robert F Engle, and Scott Murray. 2016. Empirical asset pricing: The cross section of stock returns. John Wiley & Sons.

Stulz, René M., 2018, “The Shrinking Universe of Public Firms: Facts, Causes, and Consequences”, National Bureau of Economics, 2 (June 2018)

FRM Exam Book Part I Quantative Analysis Chapter 12

Wharton Research Data Services.