Interest Rate Risk#
The essence of investment management is the management of risks, not the management of returns - Benjamin Graham
Changes in interest rates directly affect the value of bonds and fixed-income portfolios. Various measures of interest rate sensitivity, such as duration, convexity, DV01, and key rate shifts help quantify how bond prices respond to fluctations in the yield curve. Additionally, we explore the statistical approach to identifying key risk factors that explain interest rate movements.
# By: Terence Lim, 2020-2025 (terence-lim.github.io)
from typing import List
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
import statsmodels.formula.api as smf
from finds.readers import Alfred
from finds.recipes import bond_price
from secret import credentials
# %matplotlib qt
VERBOSE = 0
Interest rate sensitivity#
Duration#
Duration, or Macaulay Duration, measures how a bond’s price \( P \) changes in response to an instantaneous change in its yield \( y \).
Consider a bond with price \( P \) and yield \( y \). To simplify the duration formula, we first express the yield using continuous compounding. The bond’s price is given by:
Differentiating this equation, we obtain:
Yield-based duration is defined as the proportional change in bond price for a small change in yield:
This formulation provides an alternative interpretation of duration: it represents the weighted average time at which cash flows are received, with each time weighted by the proportion of the bond’s total value received at that time. This explains why the term “duration” is used to describe sensitivity to yield changes—duration effectively measures how long an investor must wait to receive the bond’s cash flows.
Modified duration accounts for different compounding conventions. If yields are measured with semi-annual compounding instead of continuous compounding, Macaulay duration must be adjusted by dividing by \( (1 + y_2/2) \) (or \( 1 + y_m/m \) for \( m \)-thly compounding).
Effective duration, on the other hand, measures the percentage change in the price of a bond with embedded options due to a small shift in all interest rates.
DV01#
DV01 (Dollar Value of a 01) quantifies the impact of a one-basis-point change in interest rates on a bond or portfolio’s value. It is given by:
where \( \Delta r \) represents a small parallel shift in the interest rate term structure (expressed in basis points).
Convexity#
Duration and convexity appear as the first two terms in a Taylor expansion of a bond’s price with respect to interest rates. While duration provides a linear estimate of price sensitivity, convexity measures the curvature of the bond price-yield relationship, refining estimates for larger rate movements.
Convexity accounts for the fact that bond price changes are not perfectly linear with respect to interest rate movements. Yield-based convexity, when yields are expressed with continuous compounding, is given by:
This formula represents a weighted average of the squared time to maturity. When yields are expressed with semi-annual compounding, these expressions must be divided by \( (1 + y_2/2)^2 \) (or \( (1 + y_m/m)^2 \) for \( m \)-thly compounding), and the result is known as modified convexity.
Effective convexity measures how duration itself changes in response to interest rate shifts and is calculated as:
# Helpers to calculate duration and convexity
def macaulay_duration(coupon: float, n: int, m: int, price: float,
yields: float | List[float], par: float = 1, **kwargs) -> float:
"""Compute macaulay duration of a bond given spot rates or yield-to-maturity
Args:
coupon : Annual coupon rate
n : Number of remaining coupons
m : Number of compounding periods per year
price : current market price of bond
yields : Simple annual yield-to-maturity or spot rates each period
par : face or par value of bond
Returns:
Macaulay duration
"""
if not pd.api.types.is_list_like(yields):
yields = [yields] * n # same spot rate every period
assert len(yields) == n, "Number of spot rates must equal number of couponds"
pv = [(1 + yields[t-1]/m)**(-t) * (t/m) * (coupon/m + par*(t == n))
for t in range(1, n+1)] # discount every period's time-weighted payment
return np.sum(pv) / price
def modified_duration(coupon: float, n: int, m: int, price: float,
yields: float | List[float], par: float = 1, **kwargs) -> float:
"""Compute modified duration of a bond given spot rates or yield-to-maturity
Args:
coupon : Annual coupon rate
n : Number of remaining coupons
m : Number of compounding periods per year
price : current market price of bond
yields : Simple annual yield-to-maturity or spot rates each period
par : face or par value of bond
Returns:
Modified duration
"""
assert not pd.api.types.is_list_like(yields), "Not Implemented"
ytm = yields
return (macaulay_duration(coupon=coupon, n=n, m=m, price=price, yields=yields, par=par)
/ (1 + ytm/2))
def modified_convexity(coupon: float, n: int, m: int, price: float,
yields: float | List[float], par: float = 1, **kwargs) -> float:
"""Compute mocified convexity of a bond given spot rates or yield-to-maturity
Args:
coupon : Annual coupon rate
n : Number of remaining coupons
m : Number of compounding periods per year
price : current market price of bond
yields : Simple annual yield-to-maturity or spot rates each period
par : face or par value of bond
Returns:
Modified convexity
"""
assert not pd.api.types.is_list_like(yields), "Not Implemented"
ytm = yields
if not pd.api.types.is_list_like(yields):
yields = [yields] * n # same spot rate every period
assert len(yields) == n, "Number of spot rates must equal number of coupons"
pv = [(1 + yields[t-1]/m)**(-t) * ((t/m)**2 + t/(2*m)) * (coupon/m + par*(t == n))
for t in range(1, n+1)] # discount every period's time-weighted payment
return np.sum(pv) / (price * (1 + ytm/m)**2)
Barbells and bullets#
Positive convexity benefits bondholders when there is a parallel shift in interest rates. Consider two fixed-income strategies:
A barbell strategy, which consists of holding short- and long-maturity bonds
A bullet strategy, which focuses on medium-term bonds
Both strategies may have the same yield (4%) and duration (8.1758), but the barbell strategy typically outperforms when interest rates shift in parallel. This creates an arbitrage opportunity:
Invest a given USD amount in the barbell strategy
Short the same USD amount in the bullet strategy
If term structure shifts were always parallel, this approach would be consistently profitable.
# Compute prices, duration and convexity for 3 bonds (FRM Valuation and Risk Models 12.7)
bond5Y = dict(coupon=2, m=2, n=2*5, par=100, yields=0.04)
bond10Y = dict(coupon=4, m=2, n=2*10, par=100, yields=0.04)
bond20Y = dict(coupon=6, m=2, n=2*20, par=100, yields=0.04)
for bond in [bond5Y, bond10Y, bond20Y]:
bond |= dict(price=bond_price(**bond))
bond |= dict(duration=modified_duration(**bond))
bond |= dict(convexity=modified_convexity(**bond))
bonds = DataFrame.from_dict(
{f"{b['n']/b['m']:.0f}-year, {b['coupon']}% coupon": [
b['price'], b['duration'], b['convexity']]
for b in [bond5Y, bond10Y, bond20Y]},
orient='index',
columns=['Value', 'Effective Duration', 'Effective Convexity'])
print("Table 12.4 Effective Durations and Convexities of Three Bonds")
bonds.round(4)
Table 12.4 Effective Durations and Convexities of Three Bonds
| Value | Effective Duration | Effective Convexity | |
|---|---|---|---|
| 5-year, 2% coupon | 91.0174 | 4.6764 | 24.8208 |
| 10-year, 4% coupon | 100.0000 | 8.1757 | 78.8979 |
| 20-year, 6% coupon | 127.3555 | 12.6233 | 212.4587 |
# Compute 5Y and 20Y weights of barbell portfolio, with same duration as bullet 10Y
barbell = ((bond10Y['duration'] - bond20Y['duration']) /
(bond5Y['duration'] - bond20Y['duration']))
print(f"Barbell: weight in 5Y = {barbell:.4f}, weight in 20Y = {1-barbell:.4f}")
Barbell: weight in 5Y = 0.5597, weight in 20Y = 0.4403
# Compare durations and convexities
DataFrame.from_dict(dict(Bullet=np.array([0,1,0]).dot(bonds),
Barbell=np.array([barbell, 0, 1-barbell]).dot(bonds)),
orient='index', columns=bonds.columns)\
[['Effective Duration', 'Effective Convexity']]
| Effective Duration | Effective Convexity | |
|---|---|---|
| Bullet | 8.175717 | 78.897925 |
| Barbell | 8.175717 | 107.444902 |
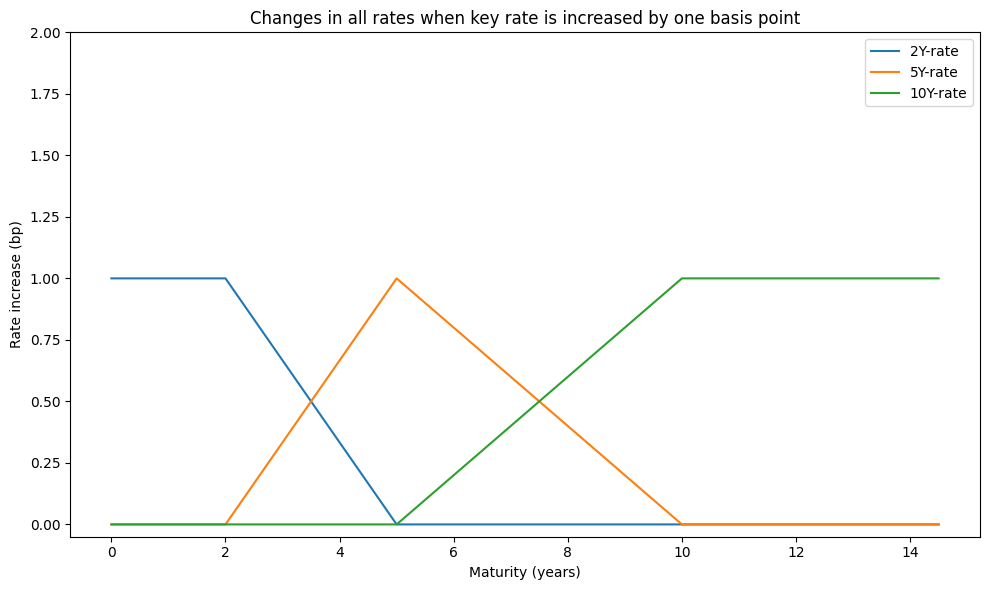
Key rate shifts#
Consider three key spot rates: the two-year, five-year, and ten-year rates. Each influences rates in its surrounding maturity range, and together, their combined movements contribute to an overall one-basis-point shift in the yield curve.
These shifts, known as key rate shifts, allow for a more detailed decomposition of DV01. The impact of these shifts is captured by partial 01s or key rate 01s (KR01s), defined as follows:
KR01₁: The reduction in portfolio value from a one-basis-point increase in the two-year spot rate
KR01₂: The reduction in portfolio value from a one-basis-point increase in the five-year spot rate
KR01₃: The reduction in portfolio value from a one-basis-point increase in the ten-year spot rate
Since these shifts sum to the overall DV01, we have:
By analyzing these key rate sensitivities, investors can better estimate portfolio values under various term structure movements and hedge against specific interest rate risks.
KR = [2, 5, 10]
DV01 = dict()
for maturity in np.arange(0, 15, 0.5):
if maturity <= KR[0]:
changes = [1, 0, 0]
elif maturity >= KR[2]:
changes = [0, 0, 1]
elif maturity < KR[1]:
diff = (maturity - KR[0])/(KR[1] - KR[0])
changes = [1 - diff, diff, 0]
else:
diff = (KR[2] - maturity)/(KR[2] - KR[1])
changes = [0, diff, 1-diff]
DV01[maturity] = changes
fig, ax = plt.subplots(figsize=(10, 6))
DataFrame.from_dict(DV01, orient='index', columns=[f"{y}Y-rate" for y in KR])\
.plot(ax=ax)
ax.legend()
ax.set_title('Changes in all rates when key rate is increased by one basis point')
ax.set_ylabel('Rate increase (bp)')
ax.set_xlabel('Maturity (years)')
ax.set_ylim(top=2)
plt.tight_layout()
Risk factors#
We examine the risk factors which drive the daily returns of the Merrill Lynch Total Bond Indexes.
alf = Alfred(api_key=credentials['fred']['api_key'], verbose=VERBOSE)
# get Merrill Lynch bond indexes
freq = 'D' # periodicity 'M' or 'D'
cat = alf.get_category(32413)
print(cat['id'], cat['name'])
32413 BofA Merrill Lynch Total Bond Return Index Values
# get bond index returns
bonds = [] # to accumulate bond returns
for s in cat['series']:
bonds.append(alf(s['id'], start=19961231, freq=freq) )
bonds_df = pd.concat(bonds, axis=1).sort_index()
# show blocks of data availability
counts = bonds_df.notna().sum(axis=1).rename('count')
counts = pd.concat([counts, (counts != counts.shift()).cumsum().rename('notna')], axis=1)
counts = counts.reset_index().groupby(['notna', 'count'])['date'].agg(['first','last'])
counts
| first | last | ||
|---|---|---|---|
| notna | count | ||
| 1 | 15 | 19961231 | 19971230 |
| 2 | 16 | 19971231 | 19981230 |
| 3 | 33 | 19981231 | 20031230 |
| 4 | 48 | 20031231 | 20181108 |
| 5 | 46 | 20181109 | 20181109 |
| 6 | 48 | 20181112 | 20250228 |
Choose start date with good data availability
start_date = 19981231
rets = bonds_df.loc[bonds_df.index >= start_date,
bonds_df.loc[start_date].notna().values].iloc[:-1]
rets = pd.concat([alf.transform(rets[col], log=1, diff=1)
for col in rets.columns], axis=1).dropna()
date_str = f" ({rets.index[0]}-{rets.index[-1]})"
rets
| BAMLCC0A0CMTRIV | BAMLCC0A1AAATRIV | BAMLCC0A2AATRIV | BAMLCC0A3ATRIV | BAMLCC0A4BBBTRIV | BAMLCC1A013YTRIV | BAMLCC2A035YTRIV | BAMLCC3A057YTRIV | BAMLCC4A0710YTRIV | BAMLCC7A01015YTRIV | ... | BAMLEMPTPRVICRPITRIV | BAMLEMRACRPIASIATRIV | BAMLEMRECRPIEMEATRIV | BAMLEMRLCRPILATRIV | BAMLEMUBCRPIUSTRIV | BAMLHE00EHYITRIV | BAMLHYH0A0HYM2TRIV | BAMLHYH0A1BBTRIV | BAMLHYH0A2BTRIV | BAMLHYH0A3CMTRIV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| date | |||||||||||||||||||||
| 19990104 | -0.001053 | -0.001421 | -0.000660 | -0.001166 | -0.000995 | 0.000076 | 0.000473 | 0.000534 | -0.000519 | -0.001209 | ... | 0.001599 | -0.000700 | -0.005616 | 0.002297 | 0.001099 | 0.000195 | 0.001490 | 0.000250 | 0.001999 | 0.003234 |
| 19990105 | -0.003846 | -0.004194 | -0.003500 | -0.003857 | -0.003952 | -0.000844 | -0.002452 | -0.003343 | -0.004276 | -0.004990 | ... | 0.002692 | 0.000400 | 0.008113 | 0.002392 | 0.002394 | 0.012287 | 0.000674 | -0.000834 | 0.000781 | 0.005428 |
| 19990106 | 0.002388 | 0.002099 | 0.002102 | 0.002495 | 0.002419 | 0.000466 | 0.000901 | 0.001695 | 0.001967 | 0.002537 | ... | 0.007144 | 0.003395 | 0.009135 | 0.006251 | 0.006060 | 0.000577 | 0.001487 | 0.001583 | 0.001041 | 0.003480 |
| 19990107 | -0.002694 | -0.002813 | -0.002413 | -0.002573 | -0.002996 | 0.000101 | -0.000853 | -0.001561 | -0.002662 | -0.003371 | ... | -0.001484 | -0.003095 | 0.007386 | 0.000198 | -0.000694 | 0.003932 | -0.000112 | -0.001250 | 0.000520 | 0.001005 |
| 19990108 | -0.002583 | -0.002941 | -0.002419 | -0.002658 | -0.002504 | -0.000920 | -0.002006 | -0.003309 | -0.003773 | -0.004368 | ... | -0.000594 | 0.001998 | 0.000392 | -0.002079 | -0.000892 | 0.000000 | 0.001737 | -0.000918 | 0.002509 | 0.007643 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20250221 | 0.004058 | 0.005418 | 0.004519 | 0.004090 | 0.003918 | 0.001278 | 0.002482 | 0.003648 | 0.004107 | 0.005264 | ... | 0.001815 | 0.002360 | 0.001548 | 0.001954 | 0.002056 | 0.000502 | -0.000726 | -0.000524 | -0.001033 | -0.000715 |
| 20250224 | 0.001879 | 0.002273 | 0.001855 | 0.001842 | 0.001917 | 0.000683 | 0.001165 | 0.001481 | 0.001797 | 0.002408 | ... | 0.001124 | 0.001355 | 0.001095 | 0.000737 | 0.001161 | 0.000422 | 0.001040 | 0.001016 | 0.001033 | 0.001213 |
| 20250225 | 0.005450 | 0.007181 | 0.006098 | 0.005468 | 0.005274 | 0.001025 | 0.002846 | 0.004326 | 0.005516 | 0.007383 | ... | 0.002267 | 0.003170 | 0.002267 | 0.002544 | 0.002939 | 0.000026 | 0.001028 | 0.001456 | 0.000758 | -0.000062 |
| 20250226 | 0.002036 | 0.002643 | 0.002200 | 0.002056 | 0.001964 | 0.000422 | 0.001190 | 0.001797 | 0.002089 | 0.002762 | ... | 0.001417 | 0.001305 | 0.001557 | 0.002419 | 0.001755 | 0.000659 | 0.001984 | 0.001797 | 0.001809 | 0.003319 |
| 20250227 | -0.002092 | -0.003094 | -0.002047 | -0.002056 | -0.002106 | 0.000216 | -0.000200 | -0.000742 | -0.001944 | -0.002688 | ... | -0.000023 | 0.000111 | 0.000705 | -0.000991 | -0.000062 | 0.000527 | -0.000006 | -0.000065 | 0.000063 | 0.000046 |
6830 rows × 33 columns
Select these bond return indexes
pd.set_option('display.max_colwidth', None)
print("Bond Index Total Returns")
Series(alf.header(rets.columns), index=rets.columns, name='title')\
.to_frame().rename_axis('series')
Bond Index Total Returns
| title | |
|---|---|
| series | |
| BAMLCC0A0CMTRIV | ICE BofA US Corporate Index Total Return Index Value |
| BAMLCC0A1AAATRIV | ICE BofA AAA US Corporate Index Total Return Index Value |
| BAMLCC0A2AATRIV | ICE BofA AA US Corporate Index Total Return Index Value |
| BAMLCC0A3ATRIV | ICE BofA Single-A US Corporate Index Total Return Index Value |
| BAMLCC0A4BBBTRIV | ICE BofA BBB US Corporate Index Total Return Index Value |
| BAMLCC1A013YTRIV | ICE BofA 1-3 Year US Corporate Index Total Return Index Value |
| BAMLCC2A035YTRIV | ICE BofA 3-5 Year US Corporate Index Total Return Index Value |
| BAMLCC3A057YTRIV | ICE BofA 5-7 Year US Corporate Index Total Return Index Value |
| BAMLCC4A0710YTRIV | ICE BofA 7-10 Year US Corporate Index Total Return Index Value |
| BAMLCC7A01015YTRIV | ICE BofA 10-15 Year US Corporate Index Total Return Index Value |
| BAMLCC8A015PYTRIV | ICE BofA 15+ Year US Corporate Index Total Return Index Value |
| BAMLEM1BRRAAA2ACRPITRIV | ICE BofA AAA-A Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEM2BRRBBBCRPITRIV | ICE BofA BBB Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEM3BRRBBCRPITRIV | ICE BofA BB Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEM4BRRBLCRPITRIV | ICE BofA B & Lower Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEM5BCOCRPITRIV | ICE BofA Crossover Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMCBPITRIV | ICE BofA Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMEBCRPIETRIV | ICE BofA Euro Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMFSFCRPITRIV | ICE BofA Private Sector Financial Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMHBHYCRPITRIV | ICE BofA High Yield Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMIBHGCRPITRIV | ICE BofA High Grade Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMNSNFCRPITRIV | ICE BofA Non-Financial Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMPBPUBSICRPITRIV | ICE BofA Public Sector Issuers Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMPTPRVICRPITRIV | ICE BofA Private Sector Issuers Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMRACRPIASIATRIV | ICE BofA Asia Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMRECRPIEMEATRIV | ICE BofA EMEA Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMRLCRPILATRIV | ICE BofA Latin America Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLEMUBCRPIUSTRIV | ICE BofA US Emerging Markets Corporate Plus Index Total Return Index Value |
| BAMLHE00EHYITRIV | ICE BofA Euro High Yield Index Total Return Index Value |
| BAMLHYH0A0HYM2TRIV | ICE BofA US High Yield Index Total Return Index Value |
| BAMLHYH0A1BBTRIV | ICE BofA BB US High Yield Index Total Return Index Value |
| BAMLHYH0A2BTRIV | ICE BofA Single-B US High Yield Index Total Return Index Value |
| BAMLHYH0A3CMTRIV | ICE BofA CCC & Lower US High Yield Index Total Return Index Value |
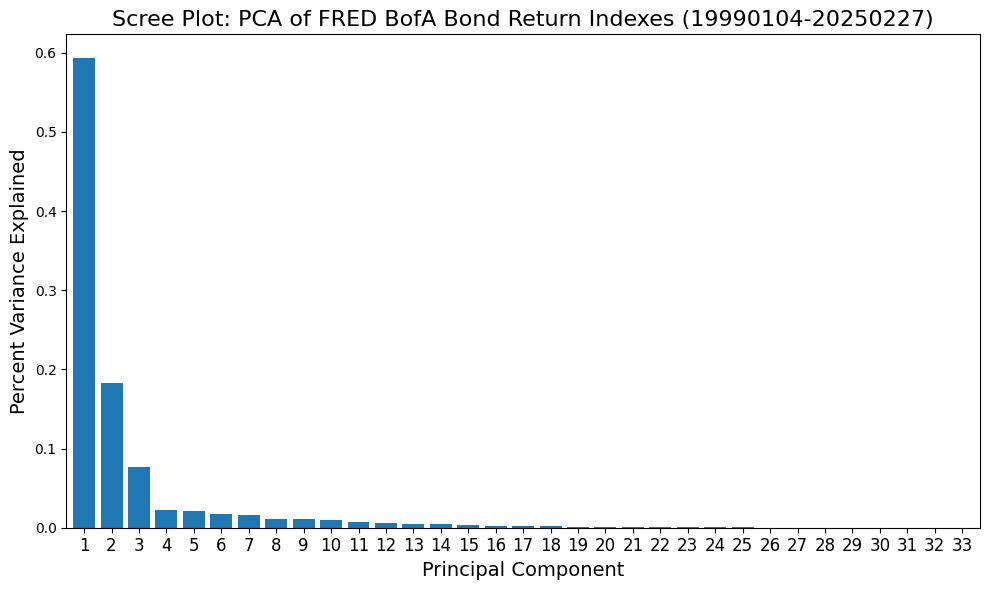
Statistical risk factors#
Extract principal components of bond index returns
pipe = Pipeline([('scaler', StandardScaler()), ('pca', PCA())])
pipe.fit(rets)
print(pipe.named_steps['pca'].explained_variance_ratio_) # sanity check
scree = Series(pipe.named_steps['pca'].explained_variance_ratio_,
index=np.arange(1, rets.shape[1]+1))
DataFrame(scree.cumsum().rename('Cumulative Variance Ratio Explained')).iloc[:10]
[5.93480704e-01 1.83414224e-01 7.60999397e-02 2.29460554e-02
2.08374926e-02 1.73252063e-02 1.58102554e-02 1.11222261e-02
1.07270153e-02 9.46337690e-03 7.12268856e-03 5.78660305e-03
5.08617829e-03 4.56329291e-03 3.87130739e-03 2.53236096e-03
2.40159698e-03 2.17255450e-03 1.28094767e-03 9.31393646e-04
7.70330791e-04 6.01123712e-04 3.93600105e-04 3.60165273e-04
3.03684121e-04 2.70804862e-04 9.27216331e-05 8.30786301e-05
5.32780919e-05 3.92254907e-05 3.55714421e-05 1.53907425e-05
5.60549950e-06]
| Cumulative Variance Ratio Explained | |
|---|---|
| 1 | 0.593481 |
| 2 | 0.776895 |
| 3 | 0.852995 |
| 4 | 0.875941 |
| 5 | 0.896778 |
| 6 | 0.914104 |
| 7 | 0.929914 |
| 8 | 0.941036 |
| 9 | 0.951763 |
| 10 | 0.961226 |
# Scree plot
fig, ax = plt.subplots(num=1, clear=True, figsize=(10, 6))
scree.plot(kind='bar', rot=0, width=.8, ax=ax)
ax.set_title('Scree Plot: PCA of FRED BofA Bond Return Indexes' + date_str, fontsize=16)
ax.xaxis.set_tick_params(labelsize=12)
ax.set_ylabel("Percent Variance Explained", fontsize=14)
ax.set_xlabel("Principal Component", fontsize=14)
plt.tight_layout()
Explainability of statistical risk factors#
# Extract factor returns from bond indexes with PCA projection
K = 4
factors = DataFrame(pipe.transform(rets)[:, :K],
columns=[f"PC{c+1}" for c in range(K)],
index=pd.DatetimeIndex(rets.index.astype(str), freq='infer'))
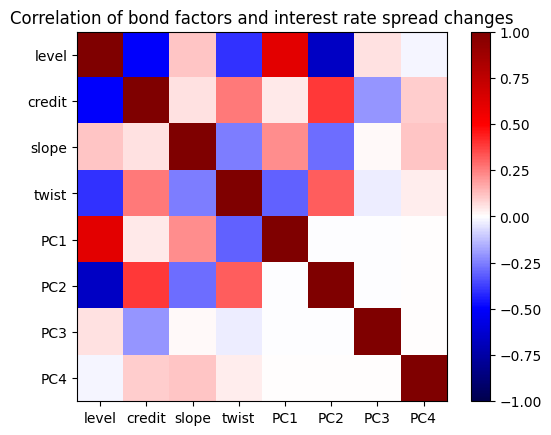
Construct interest rate spreads to compare with the statistical factors:
Level: The average of the two-year and ten-year Treasury rates
Slope: The difference between the ten-year and two-year Treasury rates
Twist: The difference between (ten-year minus five-year) and (five-year minus two-year) rates
Credit Spread: The difference between BAA corporate bond yields and ten-year Treasury rates
# Construct interest rate spread changes
spreads = pd.concat([alf(s, freq=freq) for s in ['BAA10Y', 'DGS10', 'DGS5', 'DGS2']],
axis=1)\
.sort_index()
spreads.index = pd.DatetimeIndex(spreads.index.astype(str), freq='infer')
spreads['level'] = 0.5 * (spreads['DGS2'] + spreads['DGS10'])
spreads['credit'] = spreads['BAA10Y']
spreads['slope'] = spreads['DGS10'] - spreads['DGS2']
spreads['twist'] = ((spreads['DGS10'] - spreads['DGS5']) -
(spreads['DGS5'] - spreads['DGS2']))
spreads = spreads.drop(columns=['BAA10Y', 'DGS10', 'DGS5', 'DGS2'])\
.ffill()\
.diff()\
.dropna()
spreads
| level | credit | slope | twist | |
|---|---|---|---|---|
| date | ||||
| 1986-01-03 | 0.010 | -0.04 | 1.776357e-15 | 1.776357e-15 |
| 1986-01-06 | 0.015 | -0.01 | 1.000000e-02 | -1.000000e-02 |
| 1986-01-07 | -0.100 | 0.06 | -6.000000e-02 | -8.881784e-16 |
| 1986-01-08 | 0.155 | -0.14 | 7.000000e-02 | 3.000000e-02 |
| 1986-01-09 | 0.160 | -0.05 | -4.000000e-02 | -8.000000e-02 |
| ... | ... | ... | ... | ... |
| 2025-02-24 | -0.040 | -0.01 | 4.000000e-02 | -2.000000e-02 |
| 2025-02-25 | -0.080 | 0.02 | -4.000000e-02 | 6.000000e-02 |
| 2025-02-26 | -0.035 | 0.01 | -3.000000e-02 | 5.000000e-02 |
| 2025-02-27 | 0.030 | 0.01 | 2.000000e-02 | 0.000000e+00 |
| 2025-02-28 | -0.065 | 0.05 | 3.000000e-02 | -1.000000e-02 |
9795 rows × 4 columns
# Show correlations between bond factor returns and spread changes
data = pd.concat([spreads, factors], axis=1, join='inner')
corr = data.corr()
#plt.imshow(corr**2, vmin=0, vmax=1, cmap='Purples')
plt.imshow(corr, vmin=-1, vmax=1, cmap='seismic')
plt.xticks(range(len(corr)), corr.index)
plt.yticks(range(len(corr)), corr.index)
plt.colorbar()
plt.title('Correlation of bond factors and interest rate spread changes')
Text(0.5, 1.0, 'Correlation of bond factors and interest rate spread changes')
# Show regression fits
for pc in range(K):
print(smf.ols(f"PC{pc+1} ~ credit + level + slope + twist", data=data)\
.fit(cov_type='HAC', cov_kwds={'maxlags': 63})\
.summary())
OLS Regression Results
==============================================================================
Dep. Variable: PC1 R-squared: 0.547
Model: OLS Adj. R-squared: 0.546
Method: Least Squares F-statistic: 449.8
Date: Mon, 03 Mar 2025 Prob (F-statistic): 0.00
Time: 17:15:31 Log-Likelihood: -16545.
No. Observations: 6533 AIC: 3.310e+04
Df Residuals: 6528 BIC: 3.313e+04
Df Model: 4
Covariance Type: HAC
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0260 0.089 0.293 0.770 -0.148 0.200
credit 67.2252 10.644 6.316 0.000 46.363 88.087
level 67.5805 3.099 21.810 0.000 61.507 73.654
slope 9.3162 2.473 3.767 0.000 4.469 14.164
twist -13.9266 2.182 -6.384 0.000 -18.202 -9.651
==============================================================================
Omnibus: 4287.230 Durbin-Watson: 1.169
Prob(Omnibus): 0.000 Jarque-Bera (JB): 232868.764
Skew: 2.485 Prob(JB): 0.00
Kurtosis: 31.823 Cond. No. 40.8
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity and autocorrelation robust (HAC) using 63 lags and without small sample correction
OLS Regression Results
==============================================================================
Dep. Variable: PC2 R-squared: 0.486
Model: OLS Adj. R-squared: 0.486
Method: Least Squares F-statistic: 276.0
Date: Mon, 03 Mar 2025 Prob (F-statistic): 1.62e-219
Time: 17:15:31 Log-Likelihood: -13117.
No. Observations: 6533 AIC: 2.624e+04
Df Residuals: 6528 BIC: 2.628e+04
Df Model: 4
Covariance Type: HAC
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0026 0.048 0.055 0.956 -0.092 0.097
credit 8.5003 3.413 2.491 0.013 1.811 15.190
level -27.6696 1.648 -16.794 0.000 -30.899 -24.440
slope -14.4220 1.193 -12.090 0.000 -16.760 -12.084
twist 0.0005 1.291 0.000 1.000 -2.530 2.531
==============================================================================
Omnibus: 4199.401 Durbin-Watson: 1.263
Prob(Omnibus): 0.000 Jarque-Bera (JB): 212780.844
Skew: 2.428 Prob(JB): 0.00
Kurtosis: 30.534 Cond. No. 40.8
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity and autocorrelation robust (HAC) using 63 lags and without small sample correction
OLS Regression Results
==============================================================================
Dep. Variable: PC3 R-squared: 0.048
Model: OLS Adj. R-squared: 0.048
Method: Least Squares F-statistic: 9.825
Date: Mon, 03 Mar 2025 Prob (F-statistic): 6.37e-08
Time: 17:15:32 Log-Likelihood: -12252.
No. Observations: 6533 AIC: 2.451e+04
Df Residuals: 6528 BIC: 2.455e+04
Df Model: 4
Covariance Type: HAC
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.0047 0.025 -0.189 0.850 -0.053 0.044
credit -12.9602 2.326 -5.571 0.000 -17.519 -8.401
level -2.1745 1.302 -1.671 0.095 -4.726 0.377
slope 1.7327 1.218 1.422 0.155 -0.655 4.120
twist 0.4779 1.097 0.436 0.663 -1.671 2.627
==============================================================================
Omnibus: 3598.010 Durbin-Watson: 1.563
Prob(Omnibus): 0.000 Jarque-Bera (JB): 548862.079
Skew: 1.601 Prob(JB): 0.00
Kurtosis: 47.789 Cond. No. 40.8
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity and autocorrelation robust (HAC) using 63 lags and without small sample correction
OLS Regression Results
==============================================================================
Dep. Variable: PC4 R-squared: 0.024
Model: OLS Adj. R-squared: 0.024
Method: Least Squares F-statistic: 13.23
Date: Mon, 03 Mar 2025 Prob (F-statistic): 9.77e-11
Time: 17:15:32 Log-Likelihood: -8402.4
No. Observations: 6533 AIC: 1.681e+04
Df Residuals: 6528 BIC: 1.685e+04
Df Model: 4
Covariance Type: HAC
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.0016 0.013 -0.125 0.901 -0.027 0.024
credit 2.5655 1.691 1.517 0.129 -0.748 5.879
level 0.5677 0.753 0.753 0.451 -0.909 2.044
slope 2.7974 0.428 6.532 0.000 1.958 3.637
twist 1.6629 0.452 3.679 0.000 0.777 2.549
==============================================================================
Omnibus: 2769.335 Durbin-Watson: 1.940
Prob(Omnibus): 0.000 Jarque-Bera (JB): 176343.662
Skew: 1.201 Prob(JB): 0.00
Kurtosis: 28.339 Cond. No. 40.8
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity and autocorrelation robust (HAC) using 63 lags and without small sample correction
References:
FRM Part I Exam Book Valuation and Risk Models Ch12-13