State Space Models#
If you want to understand today, you have to search yesterday - Pearl Buck
State space models provide a powerful framework for modeling time series data, particularly when the observed data are generated by an underlying system of hidden states.
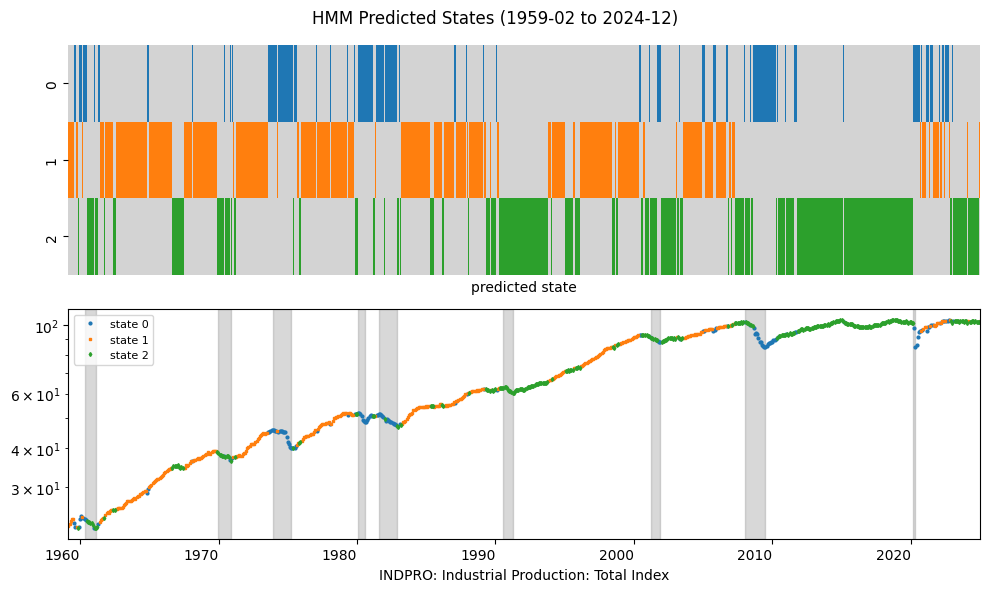
A fundamental example of a state space model is the Hidden Markov Model (HMM), which represents a system where an unobserved sequence of states follows a Markov process, and each state emits observations according to some probability distribution.
The Gaussian Mixture Model (GMM) is a probabilistic method that represents data as a combination of multiple Gaussian distributions, allowing for the estimation of the likelihood of an unknown state.
# By: Terence Lim, 2020-2025 (terence-lim.github.io)
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
import matplotlib.pyplot as plt
import seaborn as sns
from hmmlearn import hmm
from sklearn.preprocessing import StandardScaler
from sklearn.mixture import GaussianMixture
from finds.readers import fred_qd, fred_md, Alfred
from finds.recipes import approximate_factors, remove_outliers
from secret import paths, credentials
VERBOSE = 0
# %matplotlib qt
# Load and pre-process time series from FRED
alf = Alfred(api_key=credentials['fred']['api_key'], verbose=VERBOSE)
vspans = alf.date_spans('USREC') # to indicate recession periods in the plots
# FRED-MD
freq = 'M'
df, t = fred_md() if freq == 'M' else fred_qd()
transforms = t['transform']
data = pd.concat([alf.transform(df[col], tcode=transforms[col], freq=freq)
for col in df.columns],
axis=1)\
.iloc[1:] # apply transforms and drop first row
cols = list(data.columns)
# remove outliers and impute using Bai-Ng approach
r = 8 # fix number of factors = 8
data = remove_outliers(data)
data = approximate_factors(data, kmax=r, p=0, verbose=VERBOSE)
FRED-MD vintage: monthly/current.csv
# standardize inputs
X = StandardScaler().fit_transform(data.values)
Gaussian Mixture Model#
A Gaussian Mixture Model (GMM) is a probabilistic model that assumes that the data is generated from a mixture of multiple Gaussian distributions. Each component in the mixture represents a different subpopulation within the data. The following are tje parameters that need to be estimated:
Mixing Coefficients (Weights) \(\pi_k\) – These represent the proportion of each Gaussian component in the overall mixture and must sum to 1.
Mean Vectors \(\mu_k\) – The center of each Gaussian component in the feature space, indicating where each cluster is located.
Covariance Matrices \(\Sigma_k\) – These define the shape and spread of each Gaussian distribution, determining how data points are dispersed around the mean.
These parameters are typically estimated using the Expectation-Maximization (EM) algorithm, by iteratively optimizing the likelihood of the observed data.
gmm = GaussianMixture(n_components=n_components,
random_state=0,
covariance_type=best_type).fit(X)
pred_gmm = Series(gmm.predict(X),
name='state',
index=pd.to_datetime(data.index, format="%Y%m%d"))
plot_states('GMM', pred_gmm, num=2, freq=freq)
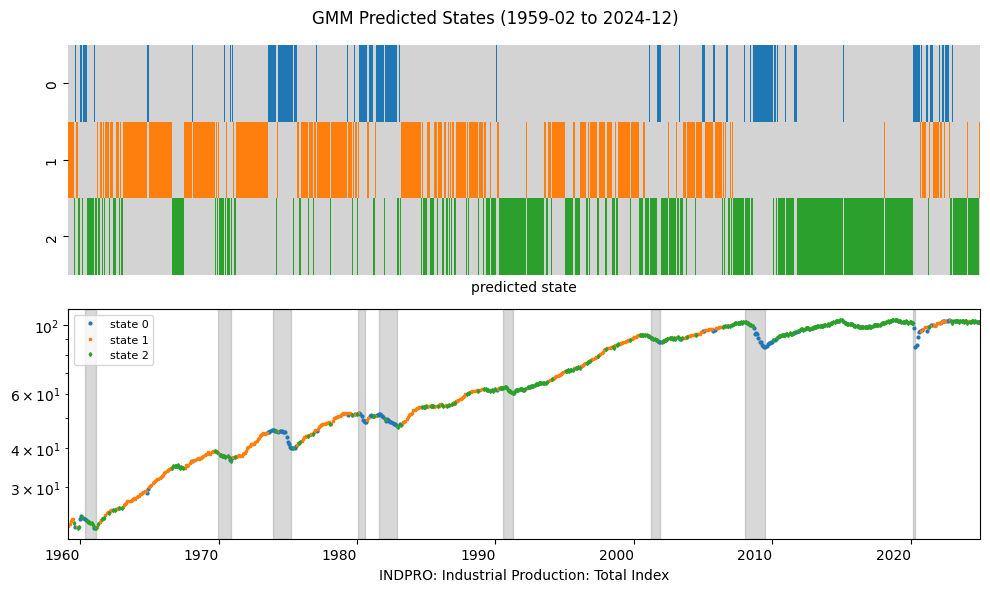
Persistance#
Persistence in an HMM refers to the likelihood that the system remains in the same hidden state over time rather than transitioning to a different state. It is determined by the self-transition probabilities on the diagonal of the transition matrix.
In GMMs, persistence refers to the likelihood of a data point belonging to the same Gaussian component across different observations. Since GMMs do not model temporal dependencies like HMMs, persistence is inferred from the posterior probability of a point belonging a particular cluster.
# Compare persistance of HMM and GMM
dist = DataFrame({
'Hidden Markov': ([np.mean(pred_markov[:-1].values == pred_markov[1:].values)]
+ matrix.iloc[:,-1].tolist()),
'Gaussian Mixture': ([np.mean(pred_gmm[:-1].values == pred_gmm[1:].values)]
+ (pred_gmm.value_counts().sort_index()/len(pred_gmm)).tolist())},
index=(['Average persistance of states']
+ [f'Stationary prob of state {s}' for s in range(n_components)]))
print("Compare HMM with GMM:")
dist
Compare HMM with GMM:
| Hidden Markov | Gaussian Mixture | |
|---|---|---|
| Average persistance of states | 0.820253 | 0.732911 |
| Stationary prob of state 0 | 0.171962 | 0.152971 |
| Stationary prob of state 1 | 0.448240 | 0.424779 |
| Stationary prob of state 2 | 0.379799 | 0.422250 |