Approximate Factor Models#
It is better to be vaguely right than precisely wrong - Carveth Read
Approximate factor models provide a simplified yet effective way to represent time series data by identifying common factors that explain variation across observed variables. A critical step in time series analysis is ensuring stationarity, typically assessed using tests like the Augmented Dickey-Fuller (ADF) test. Transformations such as differencing and logarithmic scaling are often applied to remove non-stationary components. Principal Component Analysis (PCA) is commonly used for factor extraction, and the optimal number of components can be selected using criteria like the Bayesian Information Criterion (BIC). To handle missing data, imputation methods such as the Expectation-Maximization (EM) algorithm are used.
# By: Terence Lim, 2020-2025 (terence-lim.github.io)
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from finds.readers import Alfred, fred_md, fred_qd
from finds.recipes import (approximate_factors, mrsq, select_baing, integration_order,
remove_outliers, is_outlier)
from secret import credentials
VERBOSE = 0
#%matplotlib qt
alf = Alfred(api_key=credentials['fred']['api_key'], verbose=VERBOSE)
## Retrieve recession periods from FRED
vspans = alf.date_spans('USREC')
DataFrame(vspans, columns=['Start', 'End'])
| Start | End | |
|---|---|---|
| 0 | 1854-12-31 | 1854-12-31 |
| 1 | 1857-06-30 | 1858-12-31 |
| 2 | 1860-10-31 | 1861-06-30 |
| 3 | 1865-04-30 | 1867-12-31 |
| 4 | 1869-06-30 | 1870-12-31 |
| 5 | 1873-10-31 | 1879-03-31 |
| 6 | 1882-03-31 | 1885-05-31 |
| 7 | 1887-03-31 | 1888-04-30 |
| 8 | 1890-07-31 | 1891-05-31 |
| 9 | 1893-01-31 | 1894-06-30 |
| 10 | 1895-12-31 | 1897-06-30 |
| 11 | 1899-06-30 | 1900-12-31 |
| 12 | 1902-09-30 | 1904-08-31 |
| 13 | 1907-05-31 | 1908-06-30 |
| 14 | 1910-01-31 | 1912-01-31 |
| 15 | 1913-01-31 | 1914-12-31 |
| 16 | 1918-08-31 | 1919-03-31 |
| 17 | 1920-01-31 | 1921-07-31 |
| 18 | 1923-05-31 | 1924-07-31 |
| 19 | 1926-10-31 | 1927-11-30 |
| 20 | 1929-08-31 | 1933-03-31 |
| 21 | 1937-05-31 | 1938-06-30 |
| 22 | 1945-02-28 | 1945-10-31 |
| 23 | 1948-11-30 | 1949-10-31 |
| 24 | 1953-07-31 | 1954-05-31 |
| 25 | 1957-08-31 | 1958-04-30 |
| 26 | 1960-04-30 | 1961-02-28 |
| 27 | 1969-12-31 | 1970-11-30 |
| 28 | 1973-11-30 | 1975-03-31 |
| 29 | 1980-01-31 | 1980-07-31 |
| 30 | 1981-07-31 | 1982-11-30 |
| 31 | 1990-07-31 | 1991-03-31 |
| 32 | 2001-03-31 | 2001-11-30 |
| 33 | 2007-12-31 | 2009-06-30 |
| 34 | 2020-02-29 | 2020-04-30 |
Integration order#
Augmented Dickey-Fuller test#
The Augmented Dickey-Fuller (ADF) test is one of the most widely used methods for detecting unit roots in a time series. It operates by performing an ordinary least squares (OLS) regression, where the first difference of the series is regressed on its lagged level, along with deterministic components and lagged differences. The general form of the ADF regression is:
If \(\gamma = 0 \), then \( Y_t \) follows a random walk and is non-stationary, implying the presence of a unit root. The alternative hypothesis, \( \gamma < 0 \), suggests that \( Y_t \) is covariance-stationary. This is a one-sided test, as positive values of \( \gamma \) would indicate an autoregressive coefficient greater than one, leading to instability.
When the test fails to reject the null hypothesis of a unit root, differencing is required to transform the series into a stationary form. Best practice involves repeatedly applying the ADF test to the differenced data until stationarity is achieved.
qd_df, qd_codes = fred_qd() # 202004
md_df, md_codes = fred_md() # 201505
qd_date = max(qd_df.index)
md_date = max(md_df.index)
FRED-QD vintage: quarterly/current.csv
FRED-MD vintage: monthly/current.csv
Transformations#
The FRED-MD and FRED-QD datasets include transformation codes that indicate appropriate preprocessing steps, such as applying logarithmic transformations or differencing, to ensure stationarity. The number of differences required depends on the presence of unit roots.
print(f"Number of series by suggested tcode transformations ({md_date}):")
tcodes = DataFrame.from_dict({i: alf.tcode[i] for i in range(1, 8)},
orient='index')\
.join(qd_codes['transform'].value_counts().rename('fred-qd'))\
.join(md_codes['transform'].value_counts().rename('fred-md'))\
.fillna(0)\
.astype(int)\
.rename_axis(index='tcode')
tcodes
Number of series by suggested tcode transformations (20250131):
| diff | log | pct_change | fred-qd | fred-md | |
|---|---|---|---|---|---|
| tcode | |||||
| 1 | 0 | 0 | 0 | 22 | 11 |
| 2 | 1 | 0 | 0 | 32 | 19 |
| 3 | 2 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 10 |
| 5 | 1 | 1 | 0 | 140 | 52 |
| 6 | 2 | 1 | 0 | 49 | 33 |
| 7 | 1 | 0 | 1 | 1 | 1 |
# For each series, compare fitted integration order with tcode
out = {}
stationary_out = {}
for label, df, transforms in [['md', md_df, md_codes['transform']],
['qd', qd_df, qd_codes['transform']]]:
stationary = dict()
for series_id, tcode in transforms.items():
# apply transformation if series tcode is valid
if tcode in range(1, 8):
# take logs of series if specified by tcode
s = np.log(df[series_id]) if tcode in [4, 5, 6] else df[series_id]
# estimate integration order
order = integration_order(s.dropna(), pvalue=0.05)
# expected order specified by tcode
expected_order = 2 if tcode == 7 else ((tcode - 1) % 3)
# accumulate results for this series
stationary[series_id] = {'tcode': tcode,
'I(p)': order,
'different': order - expected_order,
'title': alf.header(series_id)}
# print(series_id, tcode, expected_order, order)
# collect results for display
stationary = DataFrame.from_dict(stationary, orient='index')
stationary = stationary.sort_values(stationary.columns.to_list())
c = stationary.groupby(['tcode','I(p)'])['title'].count().reset_index()
out[label] = c.pivot(index='tcode', columns='I(p)', values='title')\
.fillna(0).astype(int)
out[label].columns=[f"I({p})" for p in out[label].columns]
stationary_out[label] = stationary[stationary['different'] > 0]
print('Series by tcode, transformations and estimated order of integration:')
results = pd.concat([tcodes.drop(columns='fred-md'),
out['qd'],
tcodes['fred-md'],
out['md']], axis=1).fillna(0).astype(int)
print('Integration order by transformation')
results
Series by tcode, transformations and estimated order of integration:
Integration order by transformation
| diff | log | pct_change | fred-qd | I(0) | I(1) | I(2) | fred-md | I(0) | I(1) | I(2) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| tcode | |||||||||||
| 1 | 0 | 0 | 0 | 22 | 17 | 5 | 0 | 11 | 11 | 0 | 0 |
| 2 | 1 | 0 | 0 | 32 | 11 | 19 | 2 | 19 | 4 | 15 | 0 |
| 3 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 10 | 7 | 3 | 0 |
| 5 | 1 | 1 | 0 | 140 | 30 | 107 | 3 | 52 | 14 | 38 | 0 |
| 6 | 2 | 1 | 0 | 49 | 0 | 29 | 20 | 33 | 0 | 30 | 3 |
| 7 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
print('FRED-MD Series with unit root after transformation')
stationary_out['md']
FRED-MD Series with unit root after transformation
| tcode | I(p) | different | title | |
|---|---|---|---|---|
| PERMITMW | 4 | 1 | 1 | New Privately-Owned Housing Units Authorized i... |
| HOUSTMW | 4 | 1 | 1 | New Privately-Owned Housing Units Started: Tot... |
| HOUSTNE | 4 | 1 | 1 | New Privately-Owned Housing Units Started: Tot... |
print('FRED-QD Series with unit root after transformation')
stationary_out['qd']
FRED-QD Series with unit root after transformation
| tcode | I(p) | different | title | |
|---|---|---|---|---|
| GS1TB3M | 1 | 1 | 1 | *** GS1TB3M *** |
| NWPI | 1 | 1 | 1 | *** NWPI *** |
| TLBSNNBBDI | 1 | 1 | 1 | *** TLBSNNBBDI *** |
| TLBSNNCBBDI | 1 | 1 | 1 | *** TLBSNNCBBDI *** |
| HWI | 1 | 1 | 1 | Help Wanted Index for United States |
| GFDEBTN | 2 | 2 | 1 | Federal Debt: Total Public Debt |
| S&P div yield | 2 | 2 | 1 | S&P's Composite Common Stock: Dividend Yield |
| CES2000000008 | 5 | 2 | 1 | Average Hourly Earnings of Production and Nons... |
| TLBSHNO | 5 | 2 | 1 | Households and Nonprofit Organizations; Total ... |
| OPHMFG | 5 | 2 | 1 | Manufacturing Sector: Labor Productivity (Outp... |
Factor selection#
Bai and Ng (2002) provide a systematic approach for extracting and determining the optimal number of factors in an approximate factor model of time series, and imputing missing or outlier observations in the dataset.
Principal component analysis (PCA)#
Principal component analysis finds a low-dimensional representation of a data set that contains as much as possible of the variation of its \(p\) features. Each principal component is a linear combination of the original features, capturing the most significant patterns in the data.
The first principal component is the normalized linear combination of features:
which maximizes variance. Subsequent principal components, such as \( Z_2 \) and \( Z_3 \), are determined iteratively, ensuring that each is uncorrelated with the previously computed components while explaining the next highest level of variance.
BIC criterion#
Determining the appropriate number of factors is a crucial step in approximate factor modeling. The Bayesian Information Criterion (BIC) selects the optimal number of components by balancing model fit and complexity. Lower BIC values indicate a better trade-off between variance explanation and model parsimony.
Data imputation#
When dealing with missing data in time series, the Expectation-Maximization (EM) algorithm can be employed to estimate missing values from factors iteratively. After each imputation iteration, factors are recovered as projections from PCA, ensuring that the underlying structure of the data is captured.
# Verify BaiNg implemention on original FRED-MD and FRED-QD
qd_df, qd_codes = fred_qd('assets/FRED-QD_2020m04.csv', url='')
md_df, md_codes = fred_md('assets/FRED-MD_2015m5.csv', url='')
for freq, df, transforms in [['monthly', md_df, md_codes['transform']],
['quarterly', qd_df, qd_codes['transform']]]:
# Apply tcode transformations
transformed = []
for col in df.columns:
transformed.append(alf.transform(df[col],
tcode=transforms[col],
freq=freq[0]))
data = pd.concat(transformed, axis=1).iloc[2:]
cols = list(data.columns)
sample = data.index[((np.count_nonzero(np.isnan(data), axis=1)==0)
| (data.index <= 20141231))
& (data.index >= 19600301)]
# set missing and outliers to NaN
x = data.loc[sample]
x = remove_outliers(x) # default fence 'iq10' is 10 times IQ
# compute factors EM and auto select number of components, r
Z = approximate_factors(x, p=2, verbose=VERBOSE)
r = select_baing(Z, p=2)
# show marginal R2's of series to each component
mR2 = mrsq(Z, r).to_numpy()
print(f"FRED-{freq[0].upper()}D {freq} series:")
print(DataFrame({'selected': r,
'variance explained': np.sum(np.mean(mR2[:, :r], axis=0)),
'start': min(sample),
'end': max(sample),
'obs': Z.shape[0],
'series': Z.shape[1]},
index=[f'factors']))
for k in range(r):
args = np.argsort(-mR2[:, k])
print(f"Factor:{1+k} Variance Explained={np.mean(mR2[:,k]):.4f}")
print(DataFrame.from_dict({mR2[arg, k].round(4):
{'series': cols[arg],
'description': alf.header(cols[arg])}
for arg in args[:10]},
orient='index'))
FRED-QD vintage: assets/FRED-QD_2020m04.csv
FRED-MD vintage: assets/FRED-MD_2015m5.csv
FRED-MD monthly series:
selected variance explained start end obs series
factors 8 0.485832 19600331 20141231 658 134
Factor:1 Variance Explained=0.1613
series description
0.7424 USGOOD All Employees, Goods-Producing
0.7235 PAYEMS All Employees, Total Nonfarm
0.7002 MANEMP All Employees, Manufacturing
0.6565 NAPM *** NAPM ***
0.6540 IPMANSICS Industrial Production: Manufacturing (SIC)
0.6513 DMANEMP All Employees, Durable Goods
0.6314 INDPRO Industrial Production: Total Index
0.6037 NAPMNOI *** NAPMNOI ***
0.6026 NAPMPI *** NAPMPI ***
0.5601 CUMFNS Capacity Utilization: Manufacturing (SIC)
Factor:2 Variance Explained=0.0703
series description
0.6259 T10YFFM 10-Year Treasury Constant Maturity Minus Feder...
0.6164 AAAFFM Moody's Seasoned Aaa Corporate Bond Minus Fede...
0.5856 BAAFFM Moody's Seasoned Baa Corporate Bond Minus Fede...
0.5832 T5YFFM 5-Year Treasury Constant Maturity Minus Federa...
0.4785 TB6SMFFM 6-Month Treasury Bill Minus Federal Funds Rate
0.4779 TB3SMFFM 3-Month Treasury Bill Minus Federal Funds Rate
0.4322 T1YFFM 1-Year Treasury Constant Maturity Minus Federa...
0.2367 COMPAPFF 3-Month Commercial Paper Minus FEDFUNDS
0.2258 BUSINV Total Business Inventories
0.1896 NAPMPRI *** NAPMPRI ***
Factor:3 Variance Explained=0.0652
series description
0.7192 CUSR0000SAC Consumer Price Index for All Urban Consumers: ...
0.7066 DNDGRG3M086SBEA Personal consumption expenditures: Nondurable ...
0.6700 CPIAUCSL Consumer Price Index for All Urban Consumers: ...
0.6392 CUSR0000SA0L5 Consumer Price Index for All Urban Consumers: ...
0.6115 CUUR0000SA0L2 Consumer Price Index for All Urban Consumers: ...
0.5923 PCEPI Personal Consumption Expenditures: Chain-type ...
0.5907 CPITRNSL Consumer Price Index for All Urban Consumers: ...
0.5482 CPIULFSL Consumer Price Index for All Urban Consumers: ...
0.4863 PPIFCG Producer Price Index by Commodity for Finished...
0.4779 PPIITM Producer Price Index by Commodity Intermediate...
Factor:4 Variance Explained=0.0547
series description
0.4294 GS1 Market Yield on U.S. Treasury Securities at 1-...
0.4228 GS5 Market Yield on U.S. Treasury Securities at 5-...
0.4123 AAA Moody's Seasoned Aaa Corporate Bond Yield
0.3995 TB6MS 6-Month Treasury Bill Secondary Market Rate, D...
0.3893 GS10 Market Yield on U.S. Treasury Securities at 10...
0.3621 BAA Moody's Seasoned Baa Corporate Bond Yield
0.3179 TB3MS 3-Month Treasury Bill Secondary Market Rate, D...
0.3139 CP3M 3-Month AA Financial Commercial Paper Rates
0.2681 HOUST New Privately-Owned Housing Units Started: Tot...
0.2562 HOUSTW New Privately-Owned Housing Units Started: Tot...
Factor:5 Variance Explained=0.0425
series description
0.2481 PERMITW New Privately-Owned Housing Units Authorized i...
0.2374 PERMIT New Privately-Owned Housing Units Authorized i...
0.2316 HOUSTW New Privately-Owned Housing Units Started: Tot...
0.2225 GS5 Market Yield on U.S. Treasury Securities at 5-...
0.2221 GS1 Market Yield on U.S. Treasury Securities at 1-...
0.2146 HOUST New Privately-Owned Housing Units Started: Tot...
0.2028 GS10 Market Yield on U.S. Treasury Securities at 10...
0.1951 PERMITMW New Privately-Owned Housing Units Authorized i...
0.1949 T1YFFM 1-Year Treasury Constant Maturity Minus Federa...
0.1932 TB6MS 6-Month Treasury Bill Secondary Market Rate, D...
Factor:6 Variance Explained=0.0365
series description
0.2186 IPCONGD Industrial Production: Consumer Goods
0.1793 ISRATIO Total Business: Inventories to Sales Ratio
0.1736 NAPMEI *** NAPMEI ***
0.1628 IPDCONGD Industrial Production: Durable Consumer Goods:...
0.1577 IPFINAL Industrial Production: Final Products
0.1545 TB6SMFFM 6-Month Treasury Bill Minus Federal Funds Rate
0.1425 NAPM *** NAPM ***
0.1416 NAPMII *** NAPMII ***
0.1414 ACOGNO Manufacturers' New Orders: Consumer Goods
0.1373 IPFPNSS Industrial Production: Final Products and Noni...
Factor:7 Variance Explained=0.0292
series description
0.5165 S&P 500 S&P's Common Stock Price Index: Composite
0.5159 S&P: indust S&P's Common Stock Price Index: Industrials
0.4002 S&P div yield S&P's Composite Common Stock: Dividend Yield
0.2764 S&P PE ratio S&P's Composite Common Stock: Price-Earnings R...
0.2564 UMCSENT University of Michigan: Consumer Sentiment
0.1030 IPCONGD Industrial Production: Consumer Goods
0.1019 EXCAUS Canadian Dollars to U.S. Dollar Spot Exchange ...
0.0728 IPFINAL Industrial Production: Final Products
0.0644 IPDCONGD Industrial Production: Durable Consumer Goods:...
0.0565 IPFPNSS Industrial Production: Final Products and Noni...
Factor:8 Variance Explained=0.0262
series description
0.5375 TWEXMMTH Nominal Major Currencies U.S. Dollar Index (Go...
0.2309 EXSZUS Swiss Francs to U.S. Dollar Spot Exchange Rate
0.2111 EXUSUK U.S. Dollars to U.K. Pound Sterling Spot Excha...
0.1497 EXJPUS Japanese Yen to U.S. Dollar Spot Exchange Rate
0.1332 SRVPRD All Employees, Service-Providing
0.1199 CES0600000008 Average Hourly Earnings of Production and Nons...
0.1156 ACOGNO Manufacturers' New Orders: Consumer Goods
0.1128 CES3000000008 Average Hourly Earnings of Production and Nons...
0.1104 USGOVT All Employees, Government
0.1010 USTRADE All Employees, Retail Trade
FRED-QD quarterly series:
selected variance explained start end obs series
factors 7 0.4981 19600331 20191231 240 248
Factor:1 Variance Explained=0.2014
series description
0.8382 USPRIV All Employees, Total Private
0.8184 USGOOD All Employees, Goods-Producing
0.8165 OUTMS Manufacturing Sector: Real Sectoral Output for...
0.8124 IPMANSICS Industrial Production: Manufacturing (SIC)
0.8120 PAYEMS All Employees, Total Nonfarm
0.8057 INDPRO Industrial Production: Total Index
0.7758 MANEMP All Employees, Manufacturing
0.7717 HOANBS Nonfarm Business Sector: Hours Worked for All ...
0.7667 DMANEMP All Employees, Durable Goods
0.7651 UNRATE Unemployment Rate
Factor:2 Variance Explained=0.0824
series description
0.4995 AAAFFM Moody's Seasoned Aaa Corporate Bond Minus Fede...
0.4761 T5YFFM 5-Year Treasury Constant Maturity Minus Federa...
0.4622 PERMIT New Privately-Owned Housing Units Authorized i...
0.4404 BUSINV Total Business Inventories
0.4231 HOUST New Privately-Owned Housing Units Started: Tot...
0.4055 PERMITS New Privately-Owned Housing Units Authorized i...
0.3925 S&P div yield S&P's Composite Common Stock: Dividend Yield
0.3849 TCU Capacity Utilization: Total Index
0.3674 CPF3MTB3M 3-Month Commercial Paper Minus 3-Month Treasur...
0.3633 GS10TB3M *** GS10TB3M ***
Factor:3 Variance Explained=0.0727
series description
0.7569 CUSR0000SA0L2 Consumer Price Index for All Urban Consumers: ...
0.7405 CUSR0000SAC Consumer Price Index for All Urban Consumers: ...
0.7368 DGDSRG3Q086SBEA Personal consumption expenditures: Goods (chai...
0.7212 PCECTPI Personal Consumption Expenditures: Chain-type ...
0.7065 CPITRNSL Consumer Price Index for All Urban Consumers: ...
0.6963 DNDGRG3Q086SBEA Personal consumption expenditures: Nondurable ...
0.6798 CUSR0000SA0L5 Consumer Price Index for All Urban Consumers: ...
0.6712 CPIAUCSL Consumer Price Index for All Urban Consumers: ...
0.6472 WPSID61 Producer Price Index by Commodity: Intermediat...
0.6352 CPIULFSL Consumer Price Index for All Urban Consumers: ...
Factor:4 Variance Explained=0.0467
series description
0.4044 IMFSL Institutional Money Market Funds (DISCONTINUED)
0.3457 CES9093000001 All Employees, Local Government
0.3259 CES9092000001 All Employees, State Government
0.2484 EXUSEU U.S. Dollars to Euro Spot Exchange Rate
0.2482 USGOVT All Employees, Government
0.2364 GFDEBTN Federal Debt: Total Public Debt
0.2251 REVOLSL Revolving Consumer Credit Owned and Securitized
0.2202 USSERV All Employees, Other Services
0.2128 COMPRMS Manufacturing Sector: Real Hourly Compensation...
0.2126 NWPI *** NWPI ***
Factor:5 Variance Explained=0.0375
series description
0.3664 OPHMFG Manufacturing Sector: Labor Productivity (Outp...
0.3093 HWI Help Wanted Index for United States
0.2989 NWPI *** NWPI ***
0.2961 AWHMAN Average Weekly Hours of Production and Nonsupe...
0.2703 OPHPBS Business Sector: Labor Productivity (Output pe...
0.2358 OPHNFB Nonfarm Business Sector: Labor Productivity (O...
0.2307 UNRATELT *** UNRATELT ***
0.2189 UNLPNBS Nonfarm Business Sector: Unit Nonlabor Payment...
0.2131 ULCMFG Manufacturing Sector: Unit Labor Costs for All...
0.1989 TLBSNNCBBDI *** TLBSNNCBBDI ***
Factor:6 Variance Explained=0.0303
series description
0.2669 CONSPI Nonrevolving consumer credit to Personal Income
0.2388 ULCBS Business Sector: Unit Labor Costs for All Workers
0.2379 ULCNFB Nonfarm Business Sector: Unit Labor Costs for ...
0.2173 CONSUMER Consumer Loans, All Commercial Banks
0.2016 EXUSEU U.S. Dollars to Euro Spot Exchange Rate
0.1979 AHETPI Average Hourly Earnings of Production and Nons...
0.1865 NONREVSL Nonrevolving Consumer Credit Owned and Securit...
0.1613 TOTALSL Total Consumer Credit Owned and Securitized
0.1453 B020RE1Q156NBEA Shares of gross domestic product: Exports of g...
0.1361 UMCSENT University of Michigan: Consumer Sentiment
Factor:7 Variance Explained=0.0270
series description
0.2663 USEPUINDXM Economic Policy Uncertainty Index for United S...
0.1954 TNWBSHNO Households and Nonprofit Organizations; Net Wo...
0.1889 TABSHNO Households and Nonprofit Organizations; Total ...
0.1872 S&P 500 S&P's Common Stock Price Index: Composite
0.1856 S&P: indust S&P's Common Stock Price Index: Industrials
0.1808 TFAABSHNO Households and Nonprofit Organizations; Total ...
0.1756 NASDAQCOM NASDAQ Composite Index
0.1623 GS10TB3M *** GS10TB3M ***
0.1394 OPHPBS Business Sector: Labor Productivity (Output pe...
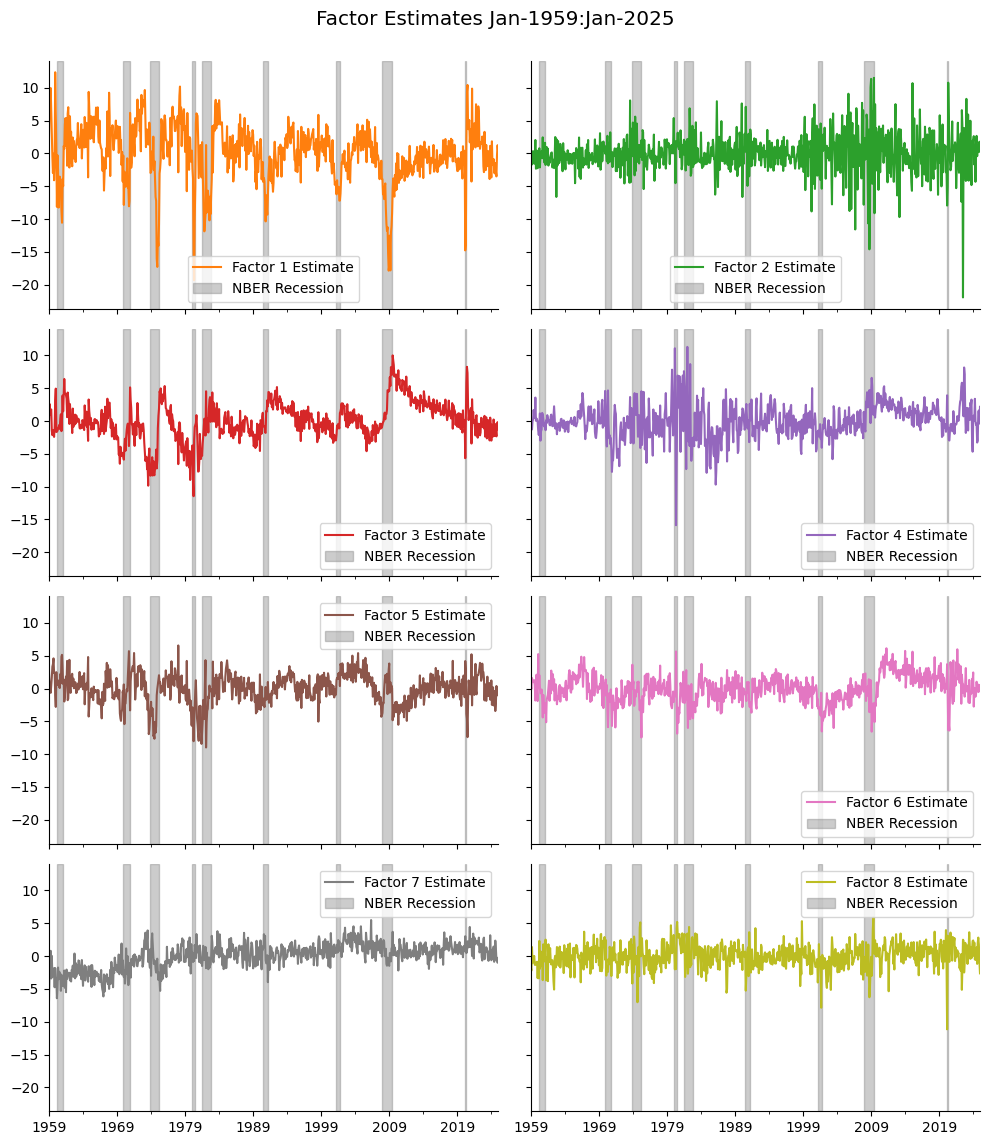
# Compute approximate factors from current FRED-MD
data, t = fred_md() # fetch dataframe of current fred-md and transform codes
data.index = pd.to_datetime(data.index, format='%Y%m%d')
transforms = t['transform']
data = pd.concat([alf.transform(data[col], tcode=transforms[col], freq='m')
for col in data.columns], axis=1)
# remove outliers and impute using Bai-Ng approach
r = 8 # fix number of factors = 8
X = remove_outliers(data, method='farout')
X = approximate_factors(X, kmax=r, p=0, verbose=VERBOSE)
FRED-MD vintage: monthly/current.csv
Recover factors as the projections from PCA
# Extract factors from PCA projections on imputed data
y = StandardScaler().fit_transform(X)
pca = PCA(n_components=r).fit(y)
factors = DataFrame(pca.transform(y), index=data.index, columns=range(1, 1+r))
# Plot extracted factors
fig, axes = plt.subplots(nrows=4, ncols=2, figsize=(10, 12), sharex=True, sharey=True)
axes = axes.flatten()
for col, ax in zip(factors.columns, axes):
flip = -np.sign(max(factors[col]) + min(factors[col])) # try match sign
(flip*factors[col]).plot(ax=ax, color=f"C{col}")
for a,b in vspans:
if b >= min(factors.index):
ax.axvspan(max(a, min(factors.index)),
min(b, max(factors.index)),
alpha=0.4,
color='grey')
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.legend([f"Factor {col} Estimate", 'NBER Recession'])
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.suptitle(f"Factor Estimates {factors.index[0]:%b-%Y}:"
f"{factors.index[-1]:%b-%Y}", fontsize='x-large')
plt.show()
References:
Bai, Jushan and Ng, Serena, 2002, Determining the Number of Factors in Approximate Factor Models, Econometrica 70:1, 191-2211
McCracken, Michael W., and Serena Ng, 2016. FRED-MD: A monthly database for macroeconomic research, Journal of Business & Economic Statistics, 34(4), 574-589.
Michael W. McCracken, Serena Ng, 2020, FRED-QD: A Quarterly Database for Macroeconomic Research.