Contrarian Trading#
Fortune befriends the bold - Emily Dickinson
Contrarian trading strategies are based on the premise of mean reversion, which posits that asset prices tend to revert to their long-term average over time. This idea is integral to various investment strategies, as it suggests that prices that have deviated significantly from historical norms will eventually return to their equilibrium levels. In these strategies, mispricing can occur due to investor overreaction, leading to temporary opportunities for profitable trades. Common approaches, such as pairs trading and statistical arbitrage, capitalize on these price deviations by simultaneously taking opposing positions in correlated assets. This analysis examines the construction of a contrarian trading strategy, evaluates its performance using key risk-adjusted metrics like the Sharpe ratio, and assesses the effects of implementation shortfall and structural breaks in the strategy’s effectiveness over time.
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
from tqdm import tqdm
import matplotlib.pyplot as plt
import rpy2.robjects as ro
from rpy2.robjects.packages import importr
from finds.database import SQL, RedisDB
from finds.structured import BusDay, CRSP, Benchmarks
from finds.recipes import fractile_split, least_squares
from finds.utils import PyR, row_formatted
from secret import credentials, paths, CRSP_DATE
VERBOSE = 0
#%matplotlib qt
importr('strucchange') # R package to use
rpy2.robjects.packages.Package as a <module 'strucchange'>
# open connections
sql = SQL(**credentials['sql'], verbose=VERBOSE)
rdb = RedisDB(**credentials['redis'])
bd = BusDay(sql, verbose=VERBOSE)
crsp = CRSP(sql, bd, rdb=rdb, verbose=VERBOSE)
bench = Benchmarks(sql, bd)
Mean reversion#
The concept of mean reversion forms the foundation of many trading strategies. According to the law of one price, similar assets should be priced similarly. When this does not hold, traders can exploit the mispricing through arbitrage by buying undervalued assets and short-selling overvalued ones, causing the prices to converge. Deviations from expected long-term values, such as yield spreads in fixed income assets, are typically not persistent. Pairs trading involves selecting two related securities and trading them to profit from their temporary price divergences. Meanwhile, statistical arbitrage (or stat arb) relies on complex algorithms to identify and exploit statistical relationships between securities. Although these relationships are not risk-free, stat arb strategies diversify across numerous positions to reduce exposure to risk. However, correlations between asset classes often increase during financial crises due to liquidity constraints and deleveraging, complicating risk management.
We evaluate a contrarian strategy based on weekly returns of US stocks, driven by the idea that stock mispricing arises from investor overreaction, as discussed by Lo and Mackinlay (1990). The alpha of this strategy can be measured by its information coefficient and volatility components, as outlined by Grinold (1994). To examine the strategy’s effectiveness over time, we apply tests for structural breaks with unknown change points. A key consideration in this analysis is the discrepancy between theoretical portfolio returns, based on assumed execution at decision prices, and actual returns, influenced by factors such as trading costs. The concept of implementation shortfall (introduced by Perold in 1988) captures the total cost of executing an investment decision, accounting for both explicit and implicit costs like market impact and opportunity costs.
Weekly returns reversals
Daily returns from CRSP are compounded in to weekly stock returns assuming Wednesday-close to Wednesday-close. This skips over weekend and holiday (which often occur over a long weekend) effects. The backtest starts in January 1974, after an expansion of the stocks universe the previous year, and excludes the smallest market cap quintile (based on NYSE breakpoints) comprising microcap stocks.
Let \(\overline{r}_{t}\) and \(\sigma_{t}\) be the cross-sectional mean and standard deviation of stock returns in week \(t\). Define \(\tilde{r}_t = r_t - \overline{r}_t\) as the vector of demeaned stock returns, and \(X_{t} = -\tilde{r}_t / \sigma_t\) as the vector of normalized scores. In other words, stocks’ “exposures” to (minus) their respective prior week’s returns are standardized to have cross-sectional variance and standard deviation equal to 1.0.
Each week, a portfolio is rebalanced to hold an amount in each stock equal to their respective exposure values divided by the number of holdings \(w_{t} = X_{t}/n\). hence the portfolio overall has unit exposure to prior week’s returns \(w_{t}^TX_{t} = 1\) and is dollar-neutral \(\sum w_{t} = \sum X_{t}/n = 0\).
This portfolio construction approach can more generally incorporate additional signals where \(X\) may be a matrix with ones in the first column and standardized signal exposures in other columns. Then each row, except the first, of \(W = (X' X)^{-1} X'\) contains stock weights of a long-short characteristic porfolio: a dollar-neutral, minimum-norm (in terms of squared weights) portfolio with unit exposure through long positions in stocks with positive exposure and short positions in stocks with negative exposure to the signal, and zero exposure to the other characteristics.
The portfolio’s realized return in the following week \(t+1\) is
that is the product of the (negative) cross-sectional correlation of stock returns times the amount of cross-sectional stock volatility at week \(t+1\).
weekday = 3 # wednesday close-to-close
bd = BusDay(sql, endweek=weekday) # Generate weekly cal
begweek = 19740102 # increased stocks coverage in CRSP in Jan 1973
endweek = bd.endwk(CRSP_DATE, -1)
rebaldates = bd.date_range(begweek, endweek, freq='weekly')
retdates = bd.date_tuples(rebaldates)
june_universe = 0 # to track date when reached a June end to update universe
year = 0 # to track new year to pre-load stocks datas in batch by year
results = []
lagged_weights = Series(dtype=float) # to track "turnover" of stock weights
for rebaldate, pastdates, nextdates in tqdm(zip(
rebaldates[1:-1], retdates[:-1], retdates[1:]), total=len(rebaldates)-1):
# screen universe each June: largest 5 size deciles
d = bd.june_universe(rebaldate)
if d != june_universe: # need next June's universe
june_universe = d # update universe every June
univ = crsp.get_universe(june_universe) # usual CRSP universe screen
univ = univ[univ['decile'] <= 8] # drop smallest quintile stocks
# retrieve new annual batch of daily prices and returns when start new year
if bd.begyr(rebaldate) != year:
year = bd.begyr(rebaldate)
prc = crsp.get_range(dataset='daily',
fields=['bidlo', 'askhi', 'prc', 'retx', 'ret'],
date_field='date',
beg=year,
end=bd.offset(bd.endyr(year), 10),
cache_mode="rw")
# get past week's returns, require price at rebalance (decision) date
past_week = prc[prc.index.get_level_values('date') == rebaldate]['prc']\
.reset_index()\
.set_index('permno')\
.join(crsp.get_ret(*pastdates).reindex(univ.index))\
.dropna()
# convert past week's returns to desired standardized portfolio weights
weights = ((past_week['ret'].mean() - past_week['ret']) /
(past_week['ret'].std(ddof=0) * len(past_week)))
# adjust past week's holdings by change stock price
lagged_weights = lagged_weights.mul(crsp.get_ret(*pastdates, field='retx')\
.reindex(lagged_weights.index)\
.fillna(0) + 1)
# compute how much to buy (or sell) to achieve desired new portfolio weights
chg_weights = pd.concat([weights, -lagged_weights], axis=1)\
.fillna(0)\
.sum(axis=1)
# calculate total abs weight as denominator for scaling turnover
total_weight = weights.abs().sum() + lagged_weights.abs().sum()
# get next week's gross returns
next_week = crsp.get_ret(*nextdates).reindex(weights.index).fillna(0)
# get next day's prices to compute one-day slippage cost
next_day = prc[prc.index.get_level_values('date') ==
bd.offset(rebaldate, 1)]\
.reset_index()\
.set_index('permno')\
.drop(columns='date')\
.reindex(chg_weights.index)
# if no trade next day, then enter position at askhi (buy) or bidlo (sell)
bidask = next_day['askhi'].where(chg_weights > 0, next_day['bidlo']).abs()
# spread is relevant askhi or bidlo divided by recorded close, minus 1
spread = next_day['prc'].where(next_day['prc'] > 0, bidask)\
.div(next_day['prc'].abs())\
.sub(1)\
.fillna(0)
# finally, trade_prc is the next day's close, or the relevent askhi or bidlo
trade_prc = next_day['prc'].where(next_day['prc'] > 0, bidask).fillna(0)
# drift is next day's trade price with dividends over today's decision price
# delay (positive is cost) will be chg_weights * drift
drift = trade_prc.div(next_day['prc'].abs())\
.mul(1 + next_day['ret'])\
.sub(1)\
.fillna(0)
# exit and enter delay should sum to chg_weights.dot(next_day['ret'])
exit1 = -lagged_weights.dot(next_day['ret'].reindex(lagged_weights.index).fillna(0))
enter1 = weights.dot(next_day['ret'].reindex(weights.index).fillna(0))
# accumulate weekly calculations
results.append(DataFrame(
{'ret': weights.dot(next_week),
'exit1': exit1,
'enter1': enter1,
'delay': chg_weights.dot(next_day['ret'].fillna(0)), # delay=enter+exit
'spread': chg_weights.dot(spread),
'slippage': chg_weights.dot(drift), # total slippage
'ic': weights.corr(next_week),
'n': len(next_week),
'beg': nextdates[0],
'end': nextdates[1],
'absweight': np.sum(weights.abs()),
'turnover': chg_weights.abs().sum()/total_weight,
'vol': next_week.std(ddof=0)},
index=[rebaldate]))
# carry forward to next week as lagged portfolio weights
lagged_weights = weights
100%|█████████▉| 2659/2660 [01:29<00:00, 29.74it/s]
# Combine accumulated computations and report
df = pd.concat(results, axis=0)
dates = df.index
df.index = pd.DatetimeIndex(df.index.astype(str))
df['net'] = df['ret'].sub(df['slippage'])
# Show summary
cols = ['ic' ,'vol', 'ret', 'slippage', 'net', 'exit1', 'enter1', 'delay',
'spread', 'turnover']
indexes = ['Information coefficient', 'Cross-sectional Volatility',
'Gross return (alpha)', 'Slippage cost', 'Net (of slippage) return',
' Exit one day delay ', ' Enter one day delay ', 'Delay cost',
'Spread cost', 'Portfolio turnover']
print(f'Summary of Weekly Mean Reversion Strategy {dates[0]}-{dates[-1]}')
pd.concat([df[cols].mean(axis=0).rename('mean'),
df[cols].std(axis=0).rename('std')], axis=1)\
.set_index(pd.Index(indexes)).round(4)
Summary of Weekly Mean Reversion Strategy 19740109-20241218
| mean | std | |
|---|---|---|
| Information coefficient | 0.0376 | 0.1022 |
| Cross-sectional Volatility | 0.0536 | 0.0191 |
| Gross return (alpha) | 0.0021 | 0.0080 |
| Slippage cost | 0.0017 | 0.0047 |
| Net (of slippage) return | 0.0005 | 0.0078 |
| Exit one day delay | -0.0003 | 0.0029 |
| Enter one day delay | 0.0006 | 0.0036 |
| Delay cost | 0.0004 | 0.0041 |
| Spread cost | 0.0013 | 0.0023 |
| Portfolio turnover | 0.7363 | 0.0407 |
Implementation shortfall#
Perold (1988) observed that the a paper portfolio based upon a well-known stock rankings system significantly outperformed the actual track record of funds that make use of the system. He defined implementation shortfall as the difference in return between a theoretical portfolio and the implemented portfolio, which captures explicit fees and commissions as well as market impact, delay and opportunity costs.
Decision price is the price at the time the investment decision was made
Arrival price is the midquote (mid-point of bid-ask prices) at the time the trader, broker or trading system received the order, or the trade decision is made.
Market drift is the amount of buys (sells) multiplied by the increase (decrease) in execution price relative to the arrival price, due to execution delay.
Delay is the adverse change in execution price relative to the decision price
Opportunity costs are the profits lost due to trades that are cancelled or not executed.
Market impact costs are bid-ask spreads as well as the amount that buying or selling moves the price against the buyer or seller
The trader’s dilemma refers to the trade-off between market drift and impact: one can trade faster with more impact to minimize market drift, or trade slower to minimize market impact but at the risk of the market drifting away.
In practice, stocks in the CRSP database are not available at finer than daily frequency, so we assume that trades are executed at the next day’s closing prices.
If stocks do not trade, we estimate execution prices based on bid-ask spreads. This approach helps address slippage and delays in execution, although transaction costs cannot be directly observed in historical backtests.
Unfortunately, stock prices in CRSP are not available at a finer than daily frequency. We adjust estimated profits for slippage by waiting a full day after the decision price then setting the execution price at the next day’s closing price, when stock market exchanges typically experience the most liquidity at the close of a trading dollar. For stocks that did not trade during that day, we assumed the desired buys are executed at the (higher) ask price and sells are executed at the (lower) bid price (in CRSP for such cases, closing bid and ask quotes are recorded and the closing price is set to the negative of the bid-ask average). This approach helps address slippage and delays in execution, although transaction costs cannot be directly observed in historical backtests.
Over the full period, much of the profitability of this version of the strategy appears to be dissipated after considering a one-day execution delay and bid-ask spreads.
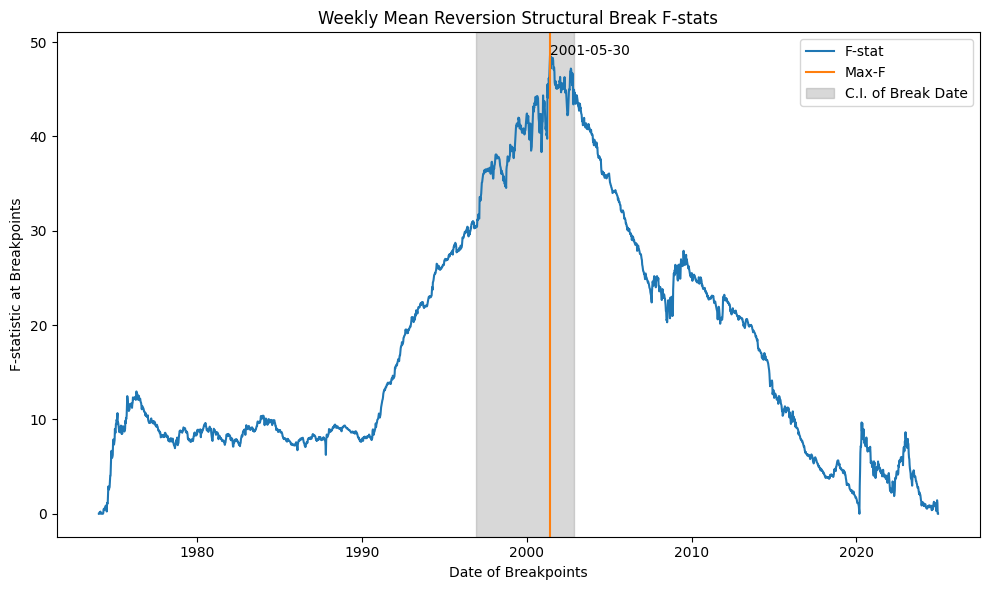
Structural break with unknown changepoint#
In a linear regression, the Chow test is commonly used to test for the presence of a structural break in the model at a period known a priori; it essentially constructs a test of whether the true coefficients on the independent variable split into two subsets are equal. Welch’s test that two populations have equal means is a special case with no independent variables and only an intercept whose true values are tested in the two time periods. However, when the breakpoints are unknown, these standard tests are not applicable. Andrews (1993) and others have developed alternative tests, based on supremum statistics, for identifying changes in mean that occur at unknown points in the time series.
The R library strucchange provides tools for detecting structural breaks, and the rpy2 Python package facilitates integration with R. The PyR wrapper class in the FinDS package facilitates converting Pandas DataFrames to and from R objects and function calls.
# Structural Break Test with Unknown Changepoint
# Set up data and formulas for R
Y = df['ret']
formula = ro.Formula('y ~ 1')
formula.environment['y'] = PyR(Y.values).ro
# Call R strucchange routines to compute breakpoint statistics
fstats_r = ro.r['Fstats'](formula, **{'from': 1}) # Fstats at every break
breakpoints_r = ro.r['breakpoints'](formula) # candidate breakpoints
confint_r = ro.r['confint'](breakpoints_r, breaks=1) # conf interval for 1 break
sctest_r = ro.r['sctest'](fstats_r, **{'type': 'aveF'})
# Extract output from R results
confint = PyR(confint_r[0]).frame.iloc[0].astype(int) - 1 # R index starts at 1
output = dict(zip(confint.index, df.index[confint])) # confidence interval
for k,v in zip(sctest_r.slots['names'][:3], sctest_r[:3]): # significance values
output[k] = PyR(v).values[0]
output['mean(pre)'] = Y[df.index <= output['breakpoints']].mean()
output['mean(post)'] = Y[df.index > output['breakpoints']].mean()
fstat = [0] + list(PyR(fstats_r[0]).values) + [0, 0] # pad before and after
print("Structural break test with unknown changepoint")
DataFrame(output, index=['sctest'])
Structural break test with unknown changepoint
| 2.5 % | breakpoints | 97.5 % | statistic | p.value | method | mean(pre) | mean(post) | |
|---|---|---|---|---|---|---|---|---|
| sctest | 1996-12-04 | 2001-05-30 | 2002-11-20 | 17.588886 | 0.0 | aveF test | 0.003112 | 0.000969 |
Plot breakpoint F-stats
fig, ax = plt.subplots(num=2, clear=True, figsize=(10, 6))
ax.plot(df.index, fstat, color='C0')
argmax = np.nanargmax(fstat) # where maximum fstat
ax.axvline(df.index[argmax], color='C1')
ax.axvspan(df.index[confint[0]], df.index[confint[2]], alpha=0.3, color='grey')
ax.legend(['F-stat', 'Max-F', 'C.I. of Break Date'])
ax.annotate(
df.index[argmax].strftime('%Y-%m-%d'), xy=(df.index[argmax], fstat[argmax]))
ax.set_ylabel('F-statistic at Breakpoints')
ax.set_xlabel('Date of Breakpoints')
ax.set_title('Weekly Mean Reversion Structural Break F-stats')
plt.tight_layout()
/tmp/ipykernel_1657351/3930510136.py:5: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
ax.axvspan(df.index[confint[0]], df.index[confint[2]], alpha=0.3, color='grey')
Performance evaluation#
Information coefficient#
Grinold (1994) linked the expected alpha of a signal to its information coefficient and an asset’s signal score and idiosyncratic volatility: \(\alpha = IC \times volatility \times score\).
IC: The information coefficient can be understood as the correlation between a signal and residual returns. It tells how well forecasts align wih actual returns and is a measure of manager forecasting skill.
Volatility: The volatility can be understood as an asset’s residual risk. This component allows for forecast alpha to be expressed in units of returns.
Score: The score is a standardized measure of an asset’s raw signal exposure, and reflects relative expectations about an asset. Standardization, by subtracing the cross-sectional mean and dividing by the cross-sectional standard deviation, allows assets to be compared to one another and over time.
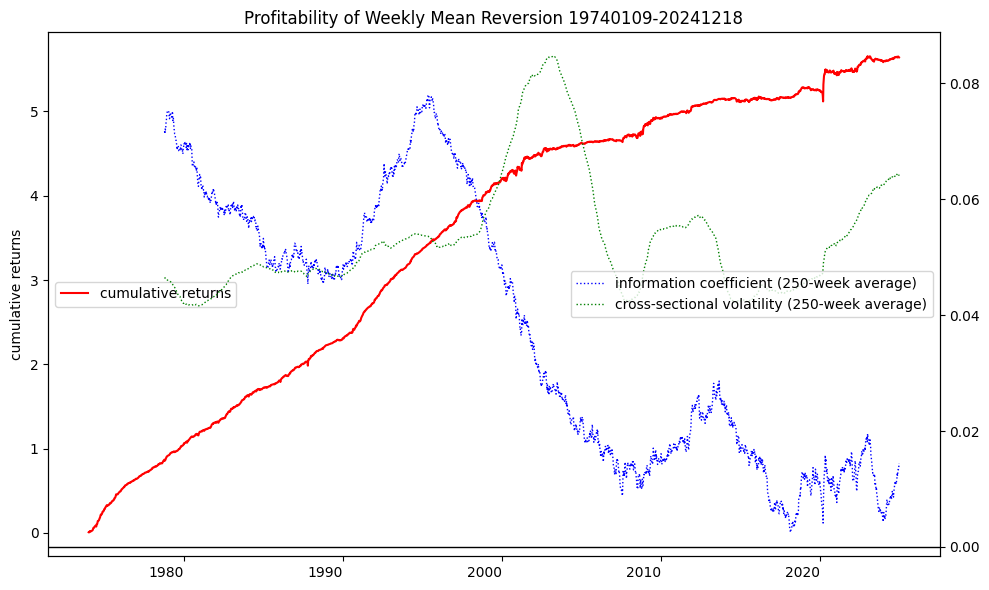
Recall that the weekly reversal portfolio \(W_t\) was constructed to be dollar-neutral with exposure equal to 1.0, with weekly profitability \(W'_t ~ r_{t+1} = -\rho_{t,t+1} ~ \sigma_{t+1}\). Hence the IC of this strategy can be computed using the negative cross-sectional correlation of stock returns over time. The rolling average of alpha and its components—information coefficient and volatility—reveal trends over the strategy’s life. The data show that while volatility fluctuated over time, the IC sharply declined after reaching a peak in the mid-1990s, continuing its downward trajectory through 2010.
## Plot returns, and rolling avg information coefficient and cross-sectional vol
fig, ax = plt.subplots(num=1, clear=True, figsize=(10, 6))
df['ret'].cumsum().plot(ax=ax, ls='-', color='r', rot=0)
ax.legend(['cumulative returns'], loc='center left')
ax.set_ylabel('cumulative returns')
bx = ax.twinx()
roll = 250 # 250 week rolling average ~ 5 years
df['ic'].rolling(roll).mean().plot(ax=bx, ls=':', lw=1, rot=0, color='b')
df['vol'].rolling(roll).mean().plot(ax=bx, ls=':', lw=1, rot=0, color='g')
#bx.axhline(df['ic'].mean(), linestyle='-', color='C0', lw=2)
bx.axhline(0, linestyle='-', color='black', lw=1)
bx.legend([f"information coefficient ({roll}-week average)",
f"cross-sectional volatility ({roll}-week average)"],
loc='center right')
ax.set_title(f'Profitability of Weekly Mean Reversion {dates[0]}-{dates[-1]}')
plt.tight_layout()
Risk-adjusted performance measures#
In a CAPM equilibrium, no investor can achieve an abnormal return, and each investment yields an identical risk-adjusted return. In the real world, assets may yield a return in excess of, or below, that which fairly compensates for their risk exposure. To assess the strategy’s risk-adjusted performance, we employ several key metrics:
Sharpe ratio - slope of the capital market line is the fair equilibrium compensation: \(\dfrac{R_P - r_f}{\sigma_P}\)
Treynor ratio - uses beta which is an approriate measure of risk for a well-diversified portfolio: \(\dfrac{R_P - r_f}{\beta_P}\)
Jensen’s alpha - the intercept of a CAPM regression should be zero in equilibrium: \(R_P - r_f- \beta_P(R_M - r_f)\)
Appraisal ratio - Jensen’s alpha scaled by the volatility of residual returns \(\dfrac{\alpha}{\sigma_{P-M}}\)
Sortino ratio - focuses on downside risk relative a target required rate of return T: \(\dfrac{R_P - T}{\sqrt{\sum_t \min(0, r_t - T)^2 / N}}\)
Information ratio - adjusts performance relative to a benchmark, called the acive return, scaled by the volatility of active returns, called tracking error: \(\dfrac{\hat{R_P} - \hat{R_B}}{\sigma_{R_P-R_B}}\)
\(M^2\) (Modigliani-squared) - imagines that the given portfolio, P, is mixed with a position in T-bills so that the resulting portfolio P* matches the volatility of the market portfolio. Because the market index and portfolio \(P^*\) have the same standard deviation, their performance may be compared by simply subtracting returns: \(R_{P^*} - R_M\)
market = bench.get_series(permnos=['Mkt-RF'], field='ret').reset_index()
breakpoint = BusDay.to_date(output['breakpoints'])
out = dict()
for select, period in zip([dates > 0, dates <= breakpoint, dates > breakpoint],
['Full', 'Pre-break', 'Post-break']):
res = df[select].copy()
res.index = dates[select]
# align market returns and compute market regression beta
#res['date'] = res.index
res['mkt'] = [(1 + market[market['date'].between(*dt)]['Mkt-RF']).prod() - 1
for dt in res[['beg','end']].itertuples(index=False)]
# model = lm(res['mkt'], res['ret'], flatten=True)
model = least_squares(data=res, y=['ret'], x=['mkt'], stdres=True)
# save df summary
out[f"{period} Period"] = {
'start date': min(res.index),
'end date': max(res.index),
'Sharpe Ratio': np.sqrt(52)*res['ret'].mean()/res['ret'].std(),
'Average Gross Return': res['ret'].mean(),
'Std Dev Returns': res['ret'].std(),
'Market Beta': model.iloc[1],
'Jensen Alpha (annualized)': model.iloc[0] * 52,
'Appraisal Ratio': np.sqrt(52) * model.iloc[0] / model.iloc[2],
'Information Coefficient': res['ic'].mean(),
'Cross-sectional Vol': res['vol'].mean(),
'Total Slippage Cost': res['slippage'].mean(),
'Spread Cost': res['spread'].mean(),
'Delay Cost': res['delay'].mean(),
' Exit Delay Cost': res['exit1'].mean(),
' Enter Delay Cost': res['enter1'].mean(),
'Average Net Return': res['net'].mean(),
'Portfolio Turnover': res['turnover'].mean(),
#'Abs Weight': res['absweight'].mean(),
'Average Num Stocks': int(res['n'].mean()),
}
# Display as formatted DataFrame
fmts = dict.fromkeys(['start date', 'end date', 'Average Num Stocks'], '{:.0f}')
print("Subperiod Performance of Weekly Reversals")
row_formatted(DataFrame(out), formats=fmts, default='{:.4f}')
Subperiod Performance of Weekly Reversals
| Full Period | Pre-break Period | Post-break Period | |
|---|---|---|---|
| start date | 19740109 | 19740109 | 20010606 |
| end date | 20241218 | 20010530 | 20241218 |
| Sharpe Ratio | 1.9185 | 3.6668 | 0.7300 |
| Average Gross Return | 0.0021 | 0.0031 | 0.0010 |
| Std Dev Returns | 0.0080 | 0.0061 | 0.0096 |
| Market Beta | 0.0898 | 0.0686 | 0.1109 |
| Jensen Alpha (annualized) | 0.1030 | 0.1566 | 0.0407 |
| Appraisal Ratio | 1.8537 | 3.6607 | 0.6140 |
| Information Coefficient | 0.0376 | 0.0578 | 0.0140 |
| Cross-sectional Vol | 0.0536 | 0.0542 | 0.0529 |
| Total Slippage Cost | 0.0017 | 0.0028 | 0.0003 |
| Spread Cost | 0.0013 | 0.0023 | 0.0002 |
| Delay Cost | 0.0004 | 0.0005 | 0.0002 |
| Exit Delay Cost | -0.0003 | -0.0004 | -0.0001 |
| Enter Delay Cost | 0.0006 | 0.0010 | 0.0002 |
| Average Net Return | 0.0005 | 0.0003 | 0.0006 |
| Portfolio Turnover | 0.7363 | 0.7393 | 0.7328 |
| Average Num Stocks | 1936 | 1981 | 1884 |
The structural break test identified a statistically significant change in the strategy’s weekly returns around mid-2001. Comparing performance before and after this point reveals a clear decline in the annualized Sharpe ratio and average weekly returns, along with an increase in risk. This shift roughly coincides with the adoption of decimalization by the New York and American Stock Exchanges on January 29, 2001, which resulted in tighter bid-ask spreads. Prior to this change, U.S. markets quoted prices in fractions, with one-sixteenth (1/16) of a dollar being the smallest allowable price increment.
R usage notes:
/usr/bin/ld: cannot find -lgfortran
collect2: error: ld returned 1 exit status
check versions are the same:
gfortran --versionandgcc --versionselect versions to be the same:
sudo update-alternatives --config gcc
References:
Andrews, D.W.K., “Tests for parameter instability and structural change with unknown change point”, Econometrica, 61 (1993), 821-856.
Grinold, Richard C., 1994, “Alpha is Volatility Times IC Times Score”, The Journal of Portfolio Management, Summer 1994, 20(4), 9-16
Lo, Andrew W. and MacKinlay, A. Craig, 1990, “When Are Contrarian Profits Due to Stock Market Overreaction?”, The Review of Financial Studies, 3(2), 175–205
Perold, Andre, 1988, “The Implementation Shortfall: Paper versus Reality”, The Journal of Portfolio Management, 14(3), 4-9