Convolutional Neural Networks#
Life can only be understood backwards; but it must be lived forwards. - Søren Kierkegaard
Convolutional Neural Networks (CNNs) are particularly effective for analyzing structured data like images and sequences. By leveraging convolutional layers, CNNs extract hierarchical patterns from raw inputs for complex tasks such as image classification and time series prediction. We explore the application of Temporal Convolutional Networks (TCNs) for capturing dependencies in economic time series. The results from modeling multiple time series data such as CPI components are compared with with classical models like Vector Autoregression (VAR).
# By: Terence Lim, 2020-2025 (terence-lim.github.io)
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
import matplotlib.pyplot as plt
import random
import torch
import torch.nn as nn
import torchinfo
from statsmodels.tsa.api import VAR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from finds.structured import BusDay
from finds.readers import Alfred
from secret import credentials
# %matplotlib qt
VERBOSE = 0
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# train-test split date
split_date = '2021-12-01' # training period up to this date
Convolutions#
Convolutional layers are memory-efficient neural network components designed to process spatially structured data, such as images. Unlike fully connected (linear) layers, which require vast numbers of parameters, convolutional layers use localized, shared filters called kernels to capture patterns in input data. Mathematically, a convolution operates as follows:
Here, \(\omega\) is a small kernel (e.g., 3×3) that slides over the image, performing element-wise multiplications and summing the results.
Image Filters#
Convolutions can be interpreted as applying image processing filters, such as:
Box filter (averaging): $\( \frac{1}{9} \begin{bmatrix} 1 & 1 & 1 \\\\ 1 & 1 & 1 \\\\ 1 & 1 & 1 \end{bmatrix} \)$
Edge detection filter: $\( \begin{bmatrix} -1 & -1 & -1 \\\\ 0 & 0 & 0 \\\\ 1 & 1 & 1 \end{bmatrix} \)$
Thus, convolutional layers serve as feature extractors, enabling models to detect edges, textures, and patterns crucial for tasks like image classification and segmentation.
Receptive field and output size#
Convolutions operate on local patches of an image, but by stacking multiple layers, they can expand their receptive field, allowing the network to capture broader context. Several parameters affect the output size and receptive field:
Padding: Adds extra pixels around the input to control output size and preserve borders.
Stride: Controls how far the filter moves across the input, affecting downsampling.
Dilation: Inserts zeros between kernel elements, expanding the receptive field without increasing parameters.
Transposed convolution (up-convolution): A learnable upsampling method used to increase output size, often employed in image segmentation models like U-Net.
Computer vision#
CNNs process images based on :
Recurring Patterns: They detect similar structures that appear across different images.
Multi-Scale Patterns: They recognize features ranging from small edges to large object shapes.
Local Invariance: They take advantage of the fact that neighboring pixels often have similar values.
Semantic Grouping: They group together pixels that belong to the same object based on shared patterns.
They excel at computer vision tasks that involve recognizing structured patterns at multiple levels of abstraction. These tasks include:
Image Classification: CNNs are highly effective at identifying what object is present in an image by detecting low-level patterns (like edges and textures) and gradually building up to high-level semantic features (like object categories).
Object Detection: By capturing patterns at various scales and identifying object parts, CNNs can localize and label multiple objects within an image, even if they vary in size or position.
Semantic Segmentation: CNNs perform well at assigning a class label to each pixel in an image by grouping together pixels that form the same object or region.
AlexNet (2012) was the first deep network to outperform non-deep vision systems, winning the ImageNet challenge competition and kicking off the Deep Learning revolution. Winning the 2015 competition, ResNet introduced shortcut “residual connections” for gradients in convolutional architectures. The U-Net (2016) model designed a symmetric hourglass-shaped architecture dsemantic segmentation, combining down-sampling to capture context with up-sampling to produce higher output resolution. More recently, Vision Transformer (ViT) models have incorporated transformer encoders by dividing images into patches, treating each patch as a token.
Temporal convolutional networks (TCN)#
Temporal Convolutional Networks (TCNs) are deep convolutional architectures designed for sequence data. They utilize causal and dilated convolutions along with residual connections to model long-range dependencies efficiently. Unlike CNNs for images, TCNs handle sequential data such as time series, text, and audio.
Causal Convolutions: Ensure that each output at time \(t\) only depends on current and past inputs — preserving the temporal order:
Dilated Convolutions: Introduce gaps between filter (kernel) elements to capture long-range dependencies without expanding filter size:
Residual Connections: Allow gradients to flow efficiently through deep networks, mitigating vanishing gradient issues:
Key hyperparameters of TCNs include:
kernel_size: Size of convolutional filter.dropout: Regularization to prevent overfitting.blocks: Number of stacked convolutional layers.dilation: Grows exponentially (e.g., 1, 2, 4, …).activation: Non-linear activation, typically ReLU.
class TCN(torch.nn.Module):
class CausalConv1dBlock(torch.nn.Module):
"""Conv1d block with ReLU, skip, dropout, dilation and padding"""
def __init__(self, in_channels, out_channels, kernel_size, dilation,
dropout):
super().__init__()
# print('kernel', kernel_size, 'dilation', dilation)
self.network = torch.nn.Sequential(
torch.nn.ConstantPad1d(((kernel_size-1)*dilation, 0), 0),
torch.nn.Conv1d(in_channels, out_channels, kernel_size,
dilation=dilation),
torch.nn.ReLU(),
torch.nn.ConstantPad1d(((kernel_size-1)*dilation, 0), 0),
torch.nn.Conv1d(out_channels, out_channels, kernel_size,
dilation=dilation),
torch.nn.ReLU(),
torch.nn.Dropout(dropout))
self.skip = lambda x: x
if in_channels != out_channels: # downsample for skip if necessary
self.skip = torch.nn.Conv1d(in_channels, out_channels, 1)
def forward(self, x):
return self.network(x) + self.skip(x) # with skip connection
def __init__(self, n_features, blocks, kernel_size, dropout):
"""TCN model by connecting multiple convolution layers"""
super().__init__()
in_channels = n_features
L = []
for dilation, hidden in enumerate(blocks):
L.append(self.CausalConv1dBlock(in_channels=in_channels,
out_channels=hidden,
kernel_size=kernel_size,
dilation=2**dilation,
dropout=dropout))
in_channels = hidden
self.network = torch.nn.Sequential(*L) if L else lambda x: x
if L:
self.classifier = torch.nn.Conv1d(in_channels, n_features, 1)
else:
self.classifier = torch.nn.Sequential(
torch.nn.ConstantPad1d((kernel_size-1, 0), 0),
torch.nn.Conv1d(in_channels, n_features, kernel_size))
def forward(self, x):
"""input is (B, n_features, L)), linear expects (B, * n_features)"""
return self.classifier(self.network(x))
def save(self, filename):
"""save model state to filename"""
return torch.save(self.state_dict(), filename)
def load(self, filename):
"""load model name from filename"""
self.load_state_dict(torch.load(filename, map_location='cpu'))
return self
Data preparation#
The dataset comprises economic time series of CPI components obtained from FRED (Federal Reserve Economic Data). The data, covering various CPI categories (e.g., food, housing, transportation), is log-transformed and differenced for stationarity and standardized using StandardScaler to mean 0 and variance 1.
alf = Alfred(api_key=credentials['fred']['api_key'], verbose=-1)
vspans = alf.date_spans('USREC') # recession periods for plots
# CPI for U.S. City Average: Monthly, Seasonally Adjusted
# https://fred.stlouisfed.org/release/tables?rid=10&eid=34483
# 'CUSR0000SEEA'
series_ids = ['CPIFABSL', 'CPIHOSSL', 'CPIAPPSL', 'CPITRNSL', 'CPIMEDSL', 'CPIOGSSL']
df = pd.concat([alf(s, log=1, diff=1) for s in series_ids], axis=1)\
.dropna()\
.sort_index()
df.index = BusDay.to_datetime(df.index)
df.index.freq = 'M' # set index to datetime type and freq = 'M'
/tmp/ipykernel_1025513/4272565358.py:9: FutureWarning: 'M' is deprecated and will be removed in a future version, please use 'ME' instead.
df.index.freq = 'M' # set index to datetime type and freq = 'M'
names = [s[s.find(':')+2:s.find(' in ')] for s in alf.header(series_ids)]
names
['Food and Beverages',
'Housing',
'Apparel',
'Transportation',
'Medical Care',
'Other Goods and Services']
# Standardize the data data
scaler = StandardScaler().fit(df)
scaled_data = DataFrame(scaler.transform(df), columns=names, index=df.index)
scaled_data
| Food and Beverages | Housing | Apparel | Transportation | Medical Care | Other Goods and Services | |
|---|---|---|---|---|---|---|
| date | ||||||
| 1967-02-28 | -1.520716 | -1.129800 | 0.533990 | 0.266586 | -0.248585 | -1.017195 |
| 1967-03-31 | -0.805655 | -1.129800 | 0.124553 | -0.267488 | -0.253160 | -0.284868 |
| 1967-04-30 | -1.522780 | -0.063784 | 0.529140 | 0.263339 | 0.988995 | -1.017195 |
| 1967-05-31 | -0.805655 | -0.067262 | 0.122142 | -0.003280 | -0.266687 | -0.286982 |
| 1967-06-30 | 1.339539 | -1.129800 | 0.524347 | -0.267488 | 0.962232 | -0.289083 |
| ... | ... | ... | ... | ... | ... | ... |
| 2024-10-31 | -0.252031 | 0.063171 | -2.110286 | -0.203592 | -0.692758 | -0.172972 |
| 2024-11-30 | -0.053379 | -0.037266 | -0.114479 | 0.027062 | -0.702581 | 0.085335 |
| 2024-12-31 | -0.180743 | -0.209529 | -0.015224 | 0.767819 | -1.058184 | -1.113129 |
| 2025-01-31 | 0.090331 | -0.037301 | -3.137367 | 0.794814 | -0.701262 | -1.822241 |
| 2025-02-28 | -0.350673 | 0.133190 | 0.934107 | -0.605692 | -0.563596 | 0.499572 |
697 rows × 6 columns
ntrain = sum(scaled_data.index < split_date)
M = scaled_data.shape[1] # M is number of time series
Training#
The TCN is trained to predict the next time step of the CPI components using past observations. Training involves splitting data into train and test sets, and using the Adam optimizer to minimize mean squared error (MSE) between predictions and actual values.
# Model training parameters
seq_len = 8 # length of each input sequence for TCN
batch_size = 16
step_size = 30 # learning rate scheduler step size
lr = 0.01 # initial learning rate
num_lr = 3
num_epochs = step_size * num_lr
results = {} # to collect evaluate results
train_loss = {}
test_loss = {}
# Form input data from training set
n_features = scaled_data.shape[1] # number of input planes
train_exs = [scaled_data.iloc[(i - seq_len):(i + 1)].values
for i in range(seq_len, ntrain)]
# train_ex should have dimension (batch size, channels, sequence length+1)
train_ex = torch.tensor(scaled_data.values[:ntrain].T)[None,:,:].float().to(device)
First, a baseline model comprising just a single 1D Conv layer is trained to predict next time step
model = torch.nn.Conv1d(n_features, n_features, kernel_size=1).to(device)
print(model)
print(torchinfo.summary(model))
modelname = "1D-Convolution"
train_loss[modelname] = []
test_loss[modelname] = []
optimizer = torch.optim.Adam(model.parameters())
loss_function = nn.MSELoss()
Conv1d(6, 6, kernel_size=(1,), stride=(1,))
=================================================================
Layer (type:depth-idx) Param #
=================================================================
Conv1d 42
=================================================================
Total params: 42
Trainable params: 42
Non-trainable params: 0
=================================================================
for epoch in range(num_epochs):
for _ in range(batch_size):
total_loss = 0.0
model.train()
model.zero_grad()
X = train_ex[:,:,:-1]
Y = train_ex[:,:,1:]
output = model(X)
loss = loss_function(output, Y) # calculated over all outputs
total_loss += float(loss)
loss.backward()
optimizer.step()
model.eval()
train_loss[modelname].append(total_loss)
X = torch.tensor(scaled_data.values.T)[None,:,:].float().to(device)
pred = model(X).cpu().detach().numpy()[0,:,:].T
test_loss[modelname] = mean_squared_error(scaled_data.values[ntrain:],
pred[ntrain-1:-1])
results[modelname] = {
'Train Error': mean_squared_error(scaled_data.values[1:ntrain],
pred[:ntrain-1]),
'Test Error': mean_squared_error(scaled_data.values[ntrain:],
pred[ntrain-1:-1])
}
Save the fitted weights to compare with classical Vector Autoregression (VAR) models.
conv1d_weights = np.vstack([model.bias.cpu().detach().numpy(),
model.weight.cpu().detach().numpy()[:,:,0].T])
Next, we train various TCN configurations, utilizing StepLR learning rate scheduler and shuffled batches, while varying:
number of layers (blocks): 1, 2
different kernel sizes: 1, 2
dropout rates: 0, 0.5.
# [1,1,0], [1,2,0], [2,1,0], [2,2,0], [1,1,0.5], [1,2,0.5], [2,1,0.5], [2,2,0.5]
for block, kernel_size, dropout in [[1,1,0], [1,2,0], [2,1,0], [2,2,0], [2,2,0.3]]:
modelname = f"TCN(b={block},k={kernel_size},d={dropout:.1f})"
train_loss[modelname] = []
test_loss[modelname] = []
# Set model, optimizer, loss function and learning rate scheduler
model = TCN(n_features=n_features,
blocks=[n_features]*block,
kernel_size=kernel_size,
dropout=dropout).to(device)
print()
print('******', modelname, '******')
print(model)
print(torchinfo.summary(model))
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
scheduler = torch.optim.lr_scheduler.StepLR(
optimizer, gamma=0.1, step_size=step_size
)
loss_function = nn.MSELoss()
# Run training loop over num_epochs with batch_size
num_epochs = step_size * num_lr
for epoch in range(num_epochs):
# shuffle indxs into batches
idxs = np.arange(len(train_exs))
random.shuffle(idxs)
batches = [idxs[i:min(len(idxs), i + batch_size)]
for i in range(0, len(idxs), batch_size)]
# train by batch
total_loss = 0.0
model.train()
for batch in batches:
# input has shape (batch_size, n_features, seq_len)
# Creating a tensor from a list of numpy.ndarrays is extremely slow.
nparray = np.array([[train_exs[idx][seq] for idx in batch]
for seq in range(seq_len+1)])
train_ex = torch.tensor(nparray).permute(1, 2, 0).float().to(device)
model.zero_grad()
X = train_ex[:,:,:-1]
Y = train_ex[:,:,1:]
output = model(X)
loss = loss_function(output, Y) # calculated over all outputs
total_loss += float(loss) / len(batches)
loss.backward()
optimizer.step()
scheduler.step()
model.eval()
train_loss[modelname].append(total_loss)
if VERBOSE and (epoch % (step_size//2)) == 0:
print(epoch, num_epochs, optimizer.param_groups[0]['lr'], total_loss)
# Compute MSE of one-period ahead forecast error in train and test sets
X = torch.tensor(scaled_data.values.T)[None,:,:].float().to(device)
pred = model(X).cpu().detach().numpy()[0,:,:].T
test_loss[modelname].append(mean_squared_error(scaled_data.values[ntrain:],
pred[ntrain-1:-1]))
results[modelname] = {
'Train Error': mean_squared_error(scaled_data.values[1:ntrain],
pred[:ntrain-1]),
'Test Error': mean_squared_error(scaled_data.values[ntrain:],
pred[ntrain-1:-1])
}
#print('Blocks:', block, 'Kernel size:', kernel_size, results[modelname])
#print(pd.concat(res, axis=1).T)
****** TCN(b=1,k=1,d=0.0) ******
TCN(
(network): Sequential(
(0): CausalConv1dBlock(
(network): Sequential(
(0): ConstantPad1d(padding=(0, 0), value=0)
(1): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
(2): ReLU()
(3): ConstantPad1d(padding=(0, 0), value=0)
(4): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
(5): ReLU()
(6): Dropout(p=0, inplace=False)
)
)
)
(classifier): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
)
=================================================================
Layer (type:depth-idx) Param #
=================================================================
TCN --
├─Sequential: 1-1 --
│ └─CausalConv1dBlock: 2-1 --
│ │ └─Sequential: 3-1 84
├─Conv1d: 1-2 42
=================================================================
Total params: 126
Trainable params: 126
Non-trainable params: 0
=================================================================
****** TCN(b=1,k=2,d=0.0) ******
TCN(
(network): Sequential(
(0): CausalConv1dBlock(
(network): Sequential(
(0): ConstantPad1d(padding=(1, 0), value=0)
(1): Conv1d(6, 6, kernel_size=(2,), stride=(1,))
(2): ReLU()
(3): ConstantPad1d(padding=(1, 0), value=0)
(4): Conv1d(6, 6, kernel_size=(2,), stride=(1,))
(5): ReLU()
(6): Dropout(p=0, inplace=False)
)
)
)
(classifier): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
)
=================================================================
Layer (type:depth-idx) Param #
=================================================================
TCN --
├─Sequential: 1-1 --
│ └─CausalConv1dBlock: 2-1 --
│ │ └─Sequential: 3-1 156
├─Conv1d: 1-2 42
=================================================================
Total params: 198
Trainable params: 198
Non-trainable params: 0
=================================================================
****** TCN(b=2,k=1,d=0.0) ******
TCN(
(network): Sequential(
(0): CausalConv1dBlock(
(network): Sequential(
(0): ConstantPad1d(padding=(0, 0), value=0)
(1): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
(2): ReLU()
(3): ConstantPad1d(padding=(0, 0), value=0)
(4): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
(5): ReLU()
(6): Dropout(p=0, inplace=False)
)
)
(1): CausalConv1dBlock(
(network): Sequential(
(0): ConstantPad1d(padding=(0, 0), value=0)
(1): Conv1d(6, 6, kernel_size=(1,), stride=(1,), dilation=(2,))
(2): ReLU()
(3): ConstantPad1d(padding=(0, 0), value=0)
(4): Conv1d(6, 6, kernel_size=(1,), stride=(1,), dilation=(2,))
(5): ReLU()
(6): Dropout(p=0, inplace=False)
)
)
)
(classifier): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
)
=================================================================
Layer (type:depth-idx) Param #
=================================================================
TCN --
├─Sequential: 1-1 --
│ └─CausalConv1dBlock: 2-1 --
│ │ └─Sequential: 3-1 84
│ └─CausalConv1dBlock: 2-2 --
│ │ └─Sequential: 3-2 84
├─Conv1d: 1-2 42
=================================================================
Total params: 210
Trainable params: 210
Non-trainable params: 0
=================================================================
****** TCN(b=2,k=2,d=0.0) ******
TCN(
(network): Sequential(
(0): CausalConv1dBlock(
(network): Sequential(
(0): ConstantPad1d(padding=(1, 0), value=0)
(1): Conv1d(6, 6, kernel_size=(2,), stride=(1,))
(2): ReLU()
(3): ConstantPad1d(padding=(1, 0), value=0)
(4): Conv1d(6, 6, kernel_size=(2,), stride=(1,))
(5): ReLU()
(6): Dropout(p=0, inplace=False)
)
)
(1): CausalConv1dBlock(
(network): Sequential(
(0): ConstantPad1d(padding=(2, 0), value=0)
(1): Conv1d(6, 6, kernel_size=(2,), stride=(1,), dilation=(2,))
(2): ReLU()
(3): ConstantPad1d(padding=(2, 0), value=0)
(4): Conv1d(6, 6, kernel_size=(2,), stride=(1,), dilation=(2,))
(5): ReLU()
(6): Dropout(p=0, inplace=False)
)
)
)
(classifier): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
)
=================================================================
Layer (type:depth-idx) Param #
=================================================================
TCN --
├─Sequential: 1-1 --
│ └─CausalConv1dBlock: 2-1 --
│ │ └─Sequential: 3-1 156
│ └─CausalConv1dBlock: 2-2 --
│ │ └─Sequential: 3-2 156
├─Conv1d: 1-2 42
=================================================================
Total params: 354
Trainable params: 354
Non-trainable params: 0
=================================================================
****** TCN(b=2,k=2,d=0.3) ******
TCN(
(network): Sequential(
(0): CausalConv1dBlock(
(network): Sequential(
(0): ConstantPad1d(padding=(1, 0), value=0)
(1): Conv1d(6, 6, kernel_size=(2,), stride=(1,))
(2): ReLU()
(3): ConstantPad1d(padding=(1, 0), value=0)
(4): Conv1d(6, 6, kernel_size=(2,), stride=(1,))
(5): ReLU()
(6): Dropout(p=0.3, inplace=False)
)
)
(1): CausalConv1dBlock(
(network): Sequential(
(0): ConstantPad1d(padding=(2, 0), value=0)
(1): Conv1d(6, 6, kernel_size=(2,), stride=(1,), dilation=(2,))
(2): ReLU()
(3): ConstantPad1d(padding=(2, 0), value=0)
(4): Conv1d(6, 6, kernel_size=(2,), stride=(1,), dilation=(2,))
(5): ReLU()
(6): Dropout(p=0.3, inplace=False)
)
)
)
(classifier): Conv1d(6, 6, kernel_size=(1,), stride=(1,))
)
=================================================================
Layer (type:depth-idx) Param #
=================================================================
TCN --
├─Sequential: 1-1 --
│ └─CausalConv1dBlock: 2-1 --
│ │ └─Sequential: 3-1 156
│ └─CausalConv1dBlock: 2-2 --
│ │ └─Sequential: 3-2 156
├─Conv1d: 1-2 42
=================================================================
Total params: 354
Trainable params: 354
Non-trainable params: 0
=================================================================
Evaluation#
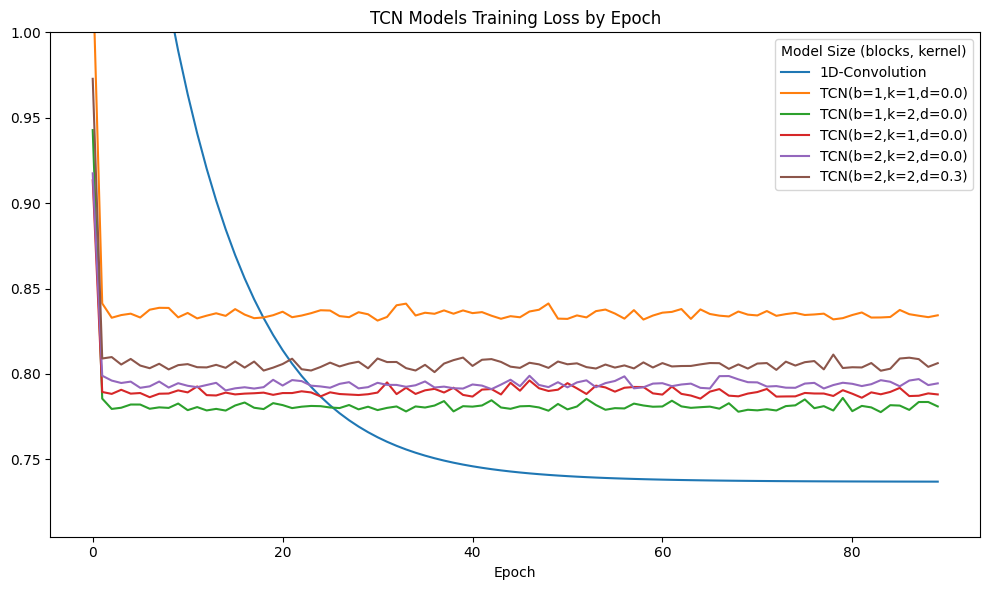
Training and test errors (MSE) from one-step-ahead forecasting are collected across models. Additionally, training and testing loss curves are plotted to analyze convergence and overfitting tendencies of different configurations.
fig, ax = plt.subplots(figsize=(10, 6))
DataFrame(train_loss).plot(ax=ax)
ax.set_ylim(top=1.0)
ax.set_title(f"TCN Models Training Loss by Epoch")
ax.set_xlabel('Epoch')
ax.legend(title='Model Size (blocks, kernel)')
plt.tight_layout()
fig, ax = plt.subplots(figsize=(10, 6))
DataFrame(test_loss).plot(ax=ax)
ax.set_ylim(top=1.0)
ax.set_title(f"TCN Models Test Loss by Epoch")
ax.set_xlabel('Epoch')
ax.legend(title='Model Size (blocks, kernel)')
plt.tight_layout()
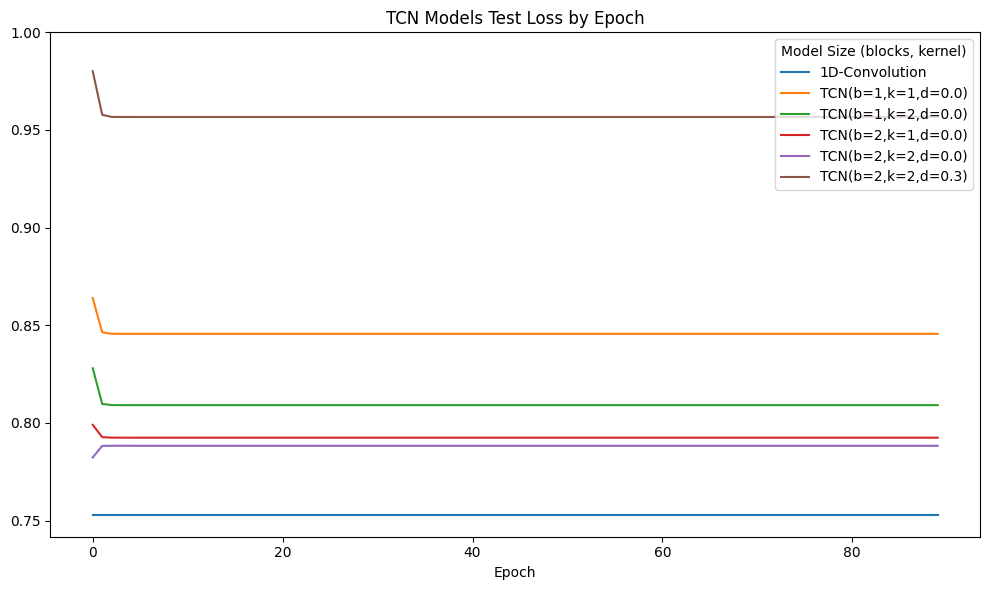
print('Sorted by Test Error')
DataFrame(results).T.sort_values('Test Error')
Sorted by Test Error
| Train Error | Test Error | |
|---|---|---|
| 1D-Convolution | 0.736907 | 0.753075 |
| TCN(b=2,k=2,d=0.0) | 0.786185 | 0.788295 |
| TCN(b=2,k=1,d=0.0) | 0.788457 | 0.792443 |
| TCN(b=1,k=2,d=0.0) | 0.775419 | 0.809113 |
| TCN(b=1,k=1,d=0.0) | 0.832984 | 0.845615 |
| TCN(b=2,k=2,d=0.3) | 0.790285 | 0.956657 |
Vector Autoregression#
Vector Autoregression (VAR) is a statistical time series model that captures linear interdependencies across multiple time series.
var_model = VAR(scaled_data.iloc[:ntrain], freq='ME')
Lag order#
The lagged coefficients estimated from the Vector Autoregression help predict multi-step future outcomes. The optimal lag order (p) can be selected using infomation criteria such as AIC, BIC, HQIC, or FPE.
# up to max number p of VAR(p) lags
maxlags = 6
print("Optimal number of VAR(p) lags selected by various IC")
DataFrame({ic: var_model.fit(maxlags=maxlags, ic=ic).k_ar
for ic in ['aic', 'fpe', 'hqic', 'bic']},
index=['optimal p:'])\
.rename_axis(columns='IC:')
Optimal number of VAR(p) lags selected by various IC
| IC: | aic | fpe | hqic | bic |
|---|---|---|---|---|
| optimal p: | 3 | 3 | 2 | 2 |
# Fit VAR(p) models
var_models = {p: var_model.fit(p) for p in range(1, maxlags+1)} # fit models
# Show model summary for VAR(1)
print(var_models[1].summary())
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Sat, 15, Mar, 2025
Time: 04:58:13
--------------------------------------------------------------------
No. of Equations: 6.00000 BIC: -1.67401
Nobs: 657.000 HQIC: -1.84967
Log likelihood: -4907.30 FPE: 0.140733
AIC: -1.96089 Det(Omega_mle): 0.132063
--------------------------------------------------------------------
Results for equation Food and Beverages
==============================================================================================
coefficient std. error t-stat prob
----------------------------------------------------------------------------------------------
const -0.000685 0.035822 -0.019 0.985
L1.Food and Beverages 0.309512 0.037889 8.169 0.000
L1.Housing 0.212849 0.043404 4.904 0.000
L1.Apparel -0.002978 0.038364 -0.078 0.938
L1.Transportation -0.006074 0.038082 -0.159 0.873
L1.Medical Care -0.007239 0.042771 -0.169 0.866
L1.Other Goods and Services 0.010009 0.037379 0.268 0.789
==============================================================================================
Results for equation Housing
==============================================================================================
coefficient std. error t-stat prob
----------------------------------------------------------------------------------------------
const -0.016126 0.027926 -0.577 0.564
L1.Food and Beverages 0.163358 0.029537 5.531 0.000
L1.Housing 0.494378 0.033836 14.611 0.000
L1.Apparel 0.038625 0.029907 1.291 0.197
L1.Transportation 0.074603 0.029687 2.513 0.012
L1.Medical Care 0.211794 0.033342 6.352 0.000
L1.Other Goods and Services -0.022649 0.029139 -0.777 0.437
==============================================================================================
Results for equation Apparel
==============================================================================================
coefficient std. error t-stat prob
----------------------------------------------------------------------------------------------
const -0.004137 0.036418 -0.114 0.910
L1.Food and Beverages 0.032202 0.038519 0.836 0.403
L1.Housing 0.108030 0.044125 2.448 0.014
L1.Apparel 0.137027 0.039002 3.513 0.000
L1.Transportation 0.187727 0.038715 4.849 0.000
L1.Medical Care 0.116103 0.043482 2.670 0.008
L1.Other Goods and Services 0.007090 0.038000 0.187 0.852
==============================================================================================
Results for equation Transportation
==============================================================================================
coefficient std. error t-stat prob
----------------------------------------------------------------------------------------------
const 0.001347 0.034599 0.039 0.969
L1.Food and Beverages 0.021051 0.036595 0.575 0.565
L1.Housing 0.070974 0.041921 1.693 0.090
L1.Apparel 0.032549 0.037054 0.878 0.380
L1.Transportation 0.425719 0.036782 11.574 0.000
L1.Medical Care 0.050082 0.041310 1.212 0.225
L1.Other Goods and Services -0.035207 0.036103 -0.975 0.329
==============================================================================================
Results for equation Medical Care
==============================================================================================
coefficient std. error t-stat prob
----------------------------------------------------------------------------------------------
const 0.033077 0.029060 1.138 0.255
L1.Food and Beverages 0.024634 0.030737 0.801 0.423
L1.Housing 0.232885 0.035211 6.614 0.000
L1.Apparel 0.044440 0.031122 1.428 0.153
L1.Transportation 0.005782 0.030893 0.187 0.852
L1.Medical Care 0.431033 0.034697 12.423 0.000
L1.Other Goods and Services 0.114476 0.030323 3.775 0.000
==============================================================================================
Results for equation Other Goods and Services
==============================================================================================
coefficient std. error t-stat prob
----------------------------------------------------------------------------------------------
const -0.009490 0.037496 -0.253 0.800
L1.Food and Beverages 0.026291 0.039660 0.663 0.507
L1.Housing 0.076689 0.045432 1.688 0.091
L1.Apparel 0.094758 0.040157 2.360 0.018
L1.Transportation 0.018115 0.039861 0.454 0.649
L1.Medical Care 0.260564 0.044769 5.820 0.000
L1.Other Goods and Services 0.009675 0.039126 0.247 0.805
==============================================================================================
Correlation matrix of residuals
Food and Beverages Housing Apparel Transportation Medical Care Other Goods and Services
Food and Beverages 1.000000 0.147358 0.085820 -0.000563 0.014162 -0.010059
Housing 0.147358 1.000000 0.093314 0.132546 0.094535 0.019075
Apparel 0.085820 0.093314 1.000000 0.126653 0.037713 0.025531
Transportation -0.000563 0.132546 0.126653 1.000000 -0.054420 -0.012936
Medical Care 0.014162 0.094535 0.037713 -0.054420 1.000000 0.153701
Other Goods and Services -0.010059 0.019075 0.025531 -0.012936 0.153701 1.000000
Var(1) and Conv1d#
The coefficients learned by VAR(1) models are compared to the learned weights of Conv1D layers, illustrating how classical linear models relate to convolution-based neural approaches in time series forecasting.
print('Coefficients of VAR(1) model')
DataFrame(np.vstack([var_models[1].intercept, var_models[1].coefs[0].T]),
columns=var_models[1].names, index=var_models[1].exog_names).round(4)
Coefficients of VAR(1) model
| Food and Beverages | Housing | Apparel | Transportation | Medical Care | Other Goods and Services | |
|---|---|---|---|---|---|---|
| const | -0.0007 | -0.0161 | -0.0041 | 0.0013 | 0.0331 | -0.0095 |
| L1.Food and Beverages | 0.3095 | 0.1634 | 0.0322 | 0.0211 | 0.0246 | 0.0263 |
| L1.Housing | 0.2128 | 0.4944 | 0.1080 | 0.0710 | 0.2329 | 0.0767 |
| L1.Apparel | -0.0030 | 0.0386 | 0.1370 | 0.0325 | 0.0444 | 0.0948 |
| L1.Transportation | -0.0061 | 0.0746 | 0.1877 | 0.4257 | 0.0058 | 0.0181 |
| L1.Medical Care | -0.0072 | 0.2118 | 0.1161 | 0.0501 | 0.4310 | 0.2606 |
| L1.Other Goods and Services | 0.0100 | -0.0226 | 0.0071 | -0.0352 | 0.1145 | 0.0097 |
print('Tensor weights of Conv1D')
DataFrame(conv1d_weights, columns=names, index=['bias'] + names).round(4)
Tensor weights of Conv1D
| Food and Beverages | Housing | Apparel | Transportation | Medical Care | Other Goods and Services | |
|---|---|---|---|---|---|---|
| bias | -0.0011 | -0.0167 | -0.0041 | 0.0014 | 0.0330 | -0.0086 |
| Food and Beverages | 0.3154 | 0.1677 | 0.0322 | 0.0210 | 0.0253 | 0.0233 |
| Housing | 0.1997 | 0.4808 | 0.1080 | 0.0713 | 0.2302 | 0.0861 |
| Apparel | -0.0014 | 0.0396 | 0.1370 | 0.0326 | 0.0447 | 0.0936 |
| Transportation | -0.0037 | 0.0773 | 0.1877 | 0.4256 | 0.0063 | 0.0166 |
| Medical Care | -0.0018 | 0.2197 | 0.1160 | 0.0493 | 0.4323 | 0.2514 |
| Other Goods and Services | 0.0105 | -0.0227 | 0.0072 | -0.0349 | 0.1146 | 0.0115 |
Evaluation#
The forecasting accuracy of VAR models, measured by train and test MSE, is compared across different lag orders.
# Calculate forecast errors for each observation and model
test_errors = {p: list() for p in range(maxlags+1)}
train_errors = {p: list() for p in range(maxlags+1)}
for i in range(maxlags, len(scaled_data)-1):
data = scaled_data.iloc[i].values
# test or train sample
var_errors = train_errors if i < ntrain else test_errors
# error of unconditional mean forecast
var_errors[0].append(mean_squared_error(data, scaled_data.iloc[:ntrain].mean()))
# accumulate to error of VAR(p) model forecasts
for p in range(1, maxlags+1):
pred = var_models[p].forecast(scaled_data.iloc[:i].values, 1)
var_errors[p].append(mean_squared_error(data.reshape(1, -1), pred))
# Collect mean test and train set errors of all VAR(p) models
print('VAR models train and test set errors')
out = DataFrame({'Train Error': {f"VAR({p})" : np.mean(errors)
for p, errors in train_errors.items()},
'Test Error': {f"VAR({p})" : np.mean(errors)
for p, errors in test_errors.items()}})
out
VAR models train and test set errors
| Train Error | Test Error | |
|---|---|---|
| VAR(0) | 1.009966 | 0.936672 |
| VAR(1) | 0.739496 | 0.757588 |
| VAR(2) | 0.696483 | 0.754189 |
| VAR(3) | 0.680224 | 0.739767 |
| VAR(4) | 0.671862 | 0.750212 |
| VAR(5) | 0.657304 | 0.739927 |
| VAR(6) | 0.647010 | 0.744329 |
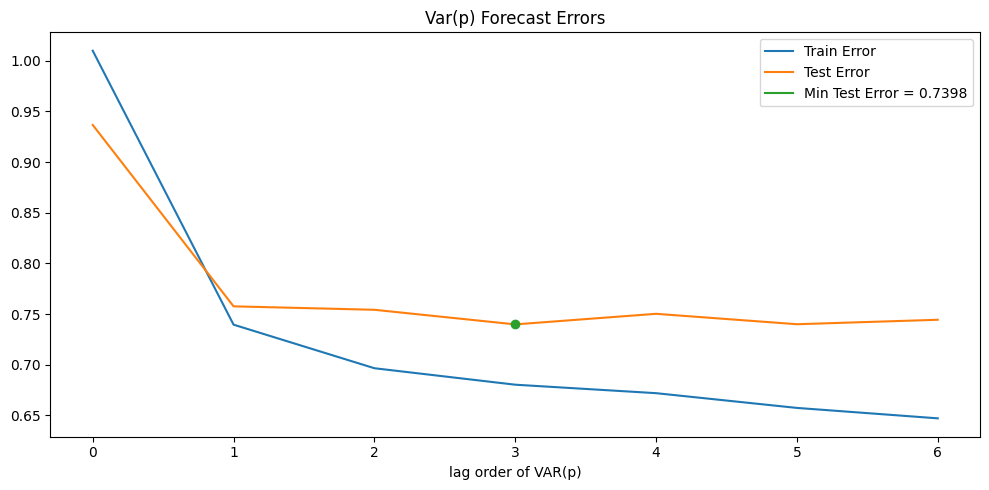
Error plots are generated to determine the optimal lag order for best predictive performance.
# Plot Errors
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(np.arange(len(out)), out['Train Error'], color="C0")
ax.plot(np.arange(len(out)), out['Test Error'], color="C1")
ax.plot([], [], color="C2") # dummy for legend labels
argmin = out['Test Error'].argmin()
ax.plot(argmin, out.iloc[argmin]['Test Error'], 'o', color="C2")
ax.set_title(f'Var(p) Forecast Errors')
ax.set_xlabel('lag order of VAR(p)')
ax.legend(['Train Error', 'Test Error',
f'Min Test Error = {out.iloc[argmin]["Test Error"]:.4f}'],
loc='upper right')
plt.tight_layout()
References:
Philipp Krähenbühl, 2020-2024, “AI394T Deep Learning course materials”, retrieved from https://www.philkr.net/dl_class/material and https://ut.philkr.net/deeplearning/
Philipp Krähenbühl, 2025, “AI395T Advances in Deep Learning course materials”, retrieved from https://ut.philkr.net/advances_in_deeplearning/