Covariance Matrix

Alone, we can do so little; together, we can do so much - Helen Keller

The covariance matrix quantifies the relationships between asset returns, enabling investors to assess diversification benefits and manage portfolio risk. We begin by exploring risk budgeting, which breaks down a portfolio’s overall risk contribution by asset, and specifically risk parity portfolios, which aim to distribute risk evenly across assets. We then cover techniques for covariance matrix estimation, including principal component analysis (PCA), Exponentially Weighted Moving Average (EWMA), and shrinkage methods.

# By: Terence Lim, 2020-2025 (terence-lim.github.io)
import numpy as np
from sklearn.decomposition import PCA
from pandas import DataFrame
import cvxpy as cp
from tqdm import tqdm
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
from sklearn.covariance import LedoitWolf, OAS, EmpiricalCovariance
from sklearn import cluster
from finds.utils import ColorMap
from finds.readers import FFReader
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)

# %matplotlib qt
VERBOSE = 0

Portfolio risk

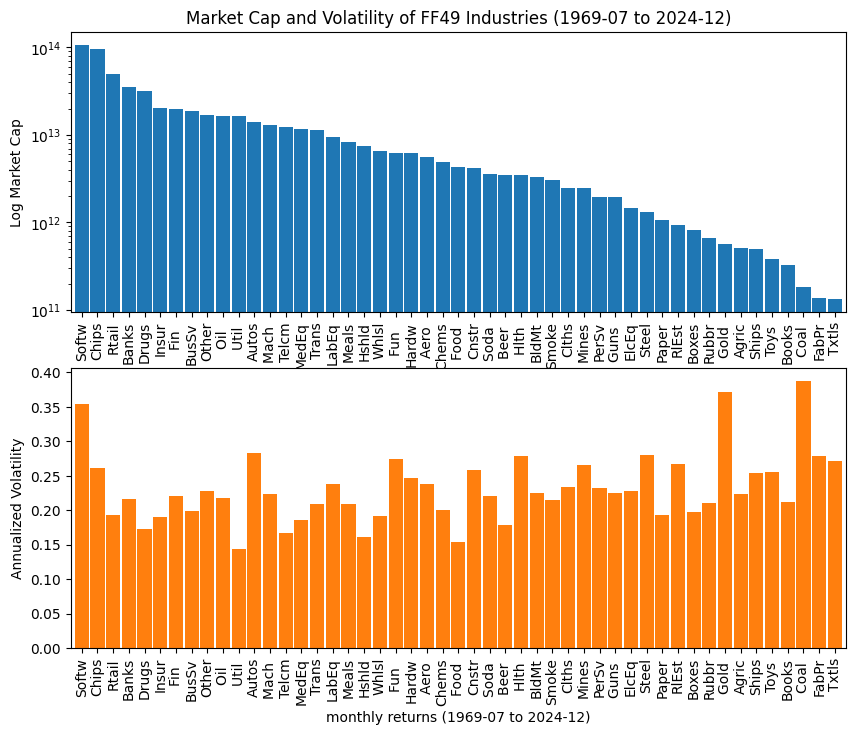
The covariance matrix is essential for portfolio risk analysis, helping investors evaluate diversification benefits and effectively manage overall risk. In this analysis, we use monthly returns from the 49 industry indexes compiled by Ken French.

# Retrieve industry returns from Ken French Data Library website
symbol = '49_Industry_Portfolios'
ff = FFReader(symbol)
keep = ff[0].index[(ff[0] > -99).all(axis=1)]
rets = (ff[0] / 100).reindex(keep)
caps = (ff[4] * ff[5] * 10e6).reindex(keep)   # number of firms x avg market cap
weights = caps.iloc[-1] / caps.iloc[-1].sum()

X = (rets - rets.mean(axis=0))    # demean by industry
sigma = 12 * X.T @ X / len(X)     # annualized covariance matrix
Y = caps.iloc[-1]\
        .rename('cap')\
        .to_frame()\
        .join(DataFrame({'vol': np.sqrt(np.diag(sigma))}, index=X.columns))\
        .sort_values('cap', ascending=False)

# Plot annualized volatility and market caps of industries
fig, ax = plt.subplots(nrows=2, figsize=(10, 8))
Y['cap'].plot.bar(ax=ax[0], color="C0", width=0.9)
ax[0].set_yscale('log')
ax[0].set_title(f"Market Cap and Volatility of FF49 Industries ({X.index[0]} to {X.index[-1]})")
ax[0].set_ylabel(f"Log Market Cap")
Y['vol'].plot.bar(ax=ax[1], color="C1", width=0.9)
ax[1].set_ylabel(f"Annualized Volatility")
ax[1].set_xlabel(f"monthly returns ({X.index[0]} to {X.index[-1]})")

Text(0.5, 0, 'monthly returns (1969-07 to 2024-12)')

Risk budgetting

Risk budgeting breaks down a portfolio’s overall risk contribution by asset.

• Portfolio Risk: The volatility of a market portfolio is given by:
  $\(\sigma_P = W^T \Sigma W\)\( where \) W \( represents the vector of asset weights in the portfolio, and \) \Sigma $ is the covariance matrix of asset returns.

• Covariance: The covariance of an individual security \( i \) with the portfolio \( P \) is expressed as:
  $\(\sigma_{iP} = \rho_{iP} \cdot \sigma_i \cdot \sigma_P\)\( where \) \rho_{iP} $ is the correlation between the security and the portfolio.

• Beta (\(\beta\)): The systematic risk of a security relative to the portfolio, defined as:
  $\(\beta_i = \dfrac{\sigma_{iP}}{\sigma_P^2}\)$
  This represents the regression slope of the security’s returns against the portfolio’s returns.

• Marginal Contribution to Risk (MCR): Measures the sensitivity of portfolio volatility to small changes in an asset’s weight:
  $\(\dfrac{\partial \sigma_P}{\partial w_i} = \dfrac{\sigma_{iP}}{\sigma_P}\)$

• Percent Contribution to Risk (PCR): Indicates the fraction of total portfolio risk attributable to a security:
  $\(\beta_i \cdot w_i\)$
  The sum of all asset contributions equals 1.

• Contribution to Portfolio Risk: The total portfolio risk can also be expressed as:
  $\(\beta_i \cdot w_i \cdot \sigma_P = w_i \cdot \sigma_i \cdot \rho_{iP}\)$ This highlights how an asset’s weight, volatility, and correlation with the portfolio drive its risk contribution.

# Helper to compute portfolio risk budget
def risk_budget(w, sigma, labels):
    """Compute portfolio risk analytics"""
    sigma_ = np.array(sigma) * 100 * 100   # express as percent returns
    w_ =  np.array(w)
    
    # Portfolio volatility (percent)
    vol = np.sqrt(w_.T @ sigma_ @ w_)
    
    # Covariance of each security wrt market portfolio
    cov = sigma_ @ w_

    # Beta of each security wrt market portfolio
    beta = cov / (w_.T @ sigma_ @ w_)

    # Marginal Contribution to Risk of each security
    marginal = beta * vol
    
    # Percent Contribution to Risk
    percent = beta * w_ * 100

    # Contribution to Risk
    contrib = marginal * w_

    return DataFrame({'weight': list(w),
                      'Beta': list(beta),
                      'MCR(%)': list(marginal),
                      'PCR(%)': list(percent),
                      'CR': list(contrib)},
                     index=labels)

vol = np.sqrt(weights.T @ sigma @ weights)  # market portfolio risk
print(f"Market Portfolio Risk Budget (vol={vol*100:.2f}%)")
risk_budget(weights, sigma, weights.index).sort_values('CR', ascending=False)

Market Portfolio Risk Budget (vol=19.34%)

	weight	Beta	MCR(%)	PCR(%)	CR
Softw	0.182276	1.555931	30.097357	28.360924	5.486032
Chips	0.161610	1.184836	22.919038	19.148127	3.703943
Rtail	0.085470	0.828755	16.031140	7.083394	1.370186
Banks	0.059413	0.843213	16.310804	5.009761	0.969070
Fin	0.033877	0.971510	18.792521	3.291171	0.636632
Drugs	0.053875	0.581038	11.239382	3.130335	0.605520
BusSv	0.031733	0.953210	18.438533	3.024847	0.585115
Other	0.028863	0.906179	17.528786	2.615469	0.505927
Insur	0.034341	0.726098	14.045377	2.493480	0.482330
Autos	0.023701	0.997867	19.302368	2.365052	0.457487
Mach	0.022131	0.974029	18.841261	2.155620	0.416975
Trans	0.019526	0.884115	17.101985	1.726316	0.333932
LabEq	0.015992	1.048768	20.286986	1.677156	0.324423
Oil	0.028253	0.592003	11.451492	1.672590	0.323540
MedEq	0.019788	0.718659	13.901468	1.422059	0.275078
Telcm	0.020845	0.597110	11.550276	1.244649	0.240760
Meals	0.014186	0.862779	16.689278	1.223961	0.236759
Fun	0.010471	1.140790	22.067019	1.194478	0.231055
Util	0.027976	0.375849	7.270286	1.051464	0.203391
Hardw	0.010442	0.988086	19.113163	1.031731	0.199574
Whlsl	0.011183	0.869373	16.816831	0.972226	0.188064
Aero	0.009449	0.927079	17.933076	0.875994	0.169449
Hshld	0.012793	0.598646	11.579978	0.765832	0.148140
Cnstr	0.007072	1.050526	20.320993	0.742934	0.143710
Chems	0.008270	0.808718	15.643534	0.668792	0.129369
Hlth	0.005851	0.968313	18.730690	0.566569	0.109595
BldMt	0.005606	0.956894	18.509810	0.536398	0.103759
Clths	0.004255	0.938755	18.158938	0.399468	0.077272
Food	0.007388	0.497495	9.623355	0.367564	0.071100
Soda	0.006012	0.610836	11.815793	0.367218	0.071033
Mines	0.004196	0.870379	16.836284	0.365172	0.070638
Beer	0.005945	0.567434	10.976238	0.337364	0.065259
PerSv	0.003352	0.919656	17.789492	0.308300	0.059636
Smoke	0.005225	0.477864	9.243631	0.249665	0.048294
ElcEq	0.002505	0.982095	18.997290	0.245969	0.047579
Steel	0.002262	1.052579	20.360697	0.238090	0.046055
Guns	0.003317	0.646421	12.504129	0.214389	0.041471
RlEst	0.001590	1.038549	20.089312	0.165107	0.031938
Paper	0.001822	0.736880	14.253940	0.134245	0.025968
Boxes	0.001378	0.731479	14.149461	0.100793	0.019497
Rubbr	0.001124	0.872047	16.868545	0.098007	0.018958
Ships	0.000854	0.858852	16.613317	0.073364	0.014191
Toys	0.000644	0.991057	19.170634	0.063808	0.012343
Agric	0.000859	0.704508	13.627738	0.060501	0.011703
Books	0.000555	0.874586	16.917676	0.048503	0.009382
Gold	0.000960	0.429793	8.313752	0.041262	0.007982
Coal	0.000311	0.879600	17.014650	0.027317	0.005284
FabPr	0.000234	0.912134	17.643973	0.021316	0.004123
Txtls	0.000225	0.946333	18.305513	0.021250	0.004111

Risk parity portfolios

A risk parity portfolio (RPP) aims to equalize the risk contribution of each asset class before leveraging to reach a target volatility. The allocation can be framed as a convex optimization problem, as proposed by Spinu (2013):
$\( \min_{w} \dfrac{1}{2} w^T \Sigma W - \sum_i b_i \log{w_i}\)\( subject to non-negative asset weights \) w_i \geq 0 \(, where \) b_i = 1/N $ represents the desired risk budget for an equally weighted risk-parity portfolio.

We use the cvxpy convex optimization package. The risk parity portfolio has the greatest weight in the Utilities industry and lowest weight in Software. By contrast, Software has the most weight in the market.

# Set up variables and constraints
N = len(sigma)
b = np.ones(N)/N            # risk parity
W = cp.Variable(N)          # portfolio weights to solve for
constraints = [W >= 0]      # non-negative weights constraint

# Solve objective
obj = 0.5 * cp.quad_form(W, sigma) - cp.sum(cp.multiply(b, cp.log(W)))  
prob = cp.Problem(cp.Minimize(obj), constraints)
prob.solve()

2.6135631335344156

# normalize solution weights
rpp = (W/cp.sum(W)).value

vol = np.sqrt(rpp.T @ sigma @ rpp)
print(f"Risk Parity Portfolio (vol={vol*100:.2f}%)")
risk_budget(rpp, sigma, weights.index).sort_values('weight', ascending=False)

Risk Parity Portfolio (vol=16.47%)

	weight	Beta	MCR(%)	PCR(%)	CR
Util	0.038404	0.531408	8.750135	2.040813	0.336039
Food	0.030511	0.668941	11.014738	2.040994	0.336069
Smoke	0.029554	0.690540	11.370397	2.040830	0.336042
Drugs	0.028845	0.707521	11.650005	2.040838	0.336043
Telcm	0.028641	0.712525	11.732403	2.040757	0.336030
Gold	0.028104	0.726190	11.957409	2.040872	0.336049
Beer	0.027832	0.733279	12.074135	2.040854	0.336046
Hshld	0.026951	0.757247	12.468779	2.040819	0.336040
Soda	0.024589	0.829944	13.665817	2.040752	0.336029
Oil	0.024289	0.840218	13.834978	2.040816	0.336040
Guns	0.023380	0.872899	14.373107	2.040875	0.336049
MedEq	0.023346	0.874162	14.393900	2.040858	0.336046
Agric	0.022982	0.888036	14.622356	2.040846	0.336045
Insur	0.021825	0.934992	15.395521	2.040612	0.336006
Rtail	0.021405	0.953405	15.698710	2.040790	0.336035
Boxes	0.021403	0.953503	15.700322	2.040788	0.336035
Paper	0.021003	0.971719	16.000274	2.040923	0.336057
Hardw	0.019636	1.039324	17.113457	2.040800	0.336037
Meals	0.019328	1.055907	17.386507	2.040808	0.336038
Banks	0.019318	1.056439	17.395264	2.040815	0.336039
Whlsl	0.019181	1.063981	17.519442	2.040796	0.336036
Chems	0.019173	1.064438	17.526974	2.040834	0.336042
Books	0.018802	1.085413	17.872354	2.040809	0.336038
Rubbr	0.018759	1.087921	17.913644	2.040859	0.336047
Other	0.018749	1.088522	17.923535	2.040857	0.336046
Trans	0.018642	1.094754	18.026153	2.040836	0.336043
BusSv	0.018231	1.119418	18.432270	2.040768	0.336032
PerSv	0.018229	1.119511	18.433801	2.040785	0.336035
Fin	0.017894	1.140526	18.779843	2.040823	0.336041
Clths	0.017822	1.145101	18.855166	2.040831	0.336042
Ships	0.017659	1.155699	19.029669	2.040855	0.336046
Aero	0.017440	1.170157	19.267736	2.040774	0.336033
Mines	0.017359	1.175643	19.358068	2.040800	0.336037
FabPr	0.017234	1.184134	19.497876	2.040778	0.336033
ElcEq	0.017124	1.191811	19.624284	2.040799	0.336037
LabEq	0.017067	1.195775	19.689563	2.040793	0.336036
Mach	0.016969	1.202645	19.802683	2.040811	0.336039
Autos	0.016837	1.212055	19.957625	2.040782	0.336034
Toys	0.016776	1.216480	20.030489	2.040790	0.336035
Chips	0.016721	1.220482	20.096388	2.040783	0.336034
BldMt	0.016630	1.227147	20.206127	2.040795	0.336036
Hlth	0.016604	1.229089	20.238114	2.040814	0.336039
Coal	0.016511	1.236048	20.352700	2.040804	0.336038
Txtls	0.016357	1.247656	20.543830	2.040811	0.336039
RlEst	0.015599	1.308309	21.542534	2.040793	0.336036
Cnstr	0.015534	1.313753	21.632185	2.040810	0.336039
Fun	0.015339	1.330599	21.909558	2.040955	0.336062
Steel	0.015297	1.334155	21.968126	2.040802	0.336037
Softw	0.014115	1.445795	23.806377	2.040797	0.336037

Covariance matrix estimation

The simplest way to estimate the covariance matrix is to calculate the average product of return deviations for each pair of assets. Additionally, we examine other techniques designed to improve estimation accuracy, particularly in high-dimensional settings.

Principal components

By retaining only the largest principal components, the Principal Component Analysis (PCA) method provides a lower-dimensional but more stable approximation of the covariance matrix that captures most of the data’s variability.

Each principal component (PC) can be interpreted as a weighted portfolio of industry assets. The projection of industry returns onto a given component effectively computes the returns of the corresponding portfolio.

# Fit PCA
pca = PCA().fit(X)

# Retrieve components, and sign flip if necessary
loadings = (np.diag(pca.singular_values_) @ pca.components_).T  # compute loadings by column
components = DataFrame.from_records(pca.components_.T, index=X.columns)
components *= np.sign(components.sum(axis=0))

# Compute projections, can be interpreted as portfolio returns
proj = pca.transform(X)
proj *= np.sign(np.sum(pca.components_, axis=1))  # flip signs if necessary

# Equal weighted market average return
avg = X.mean(axis=1)

From the summaries of the weights, the first principal component (PC1) resembles a broadly diversified portfolio, capturing more than half of the total variance. Higher-order principal components represent long-short spread portfolios, which explain incremental variance.

K = 20
print(f"Top {K} principal components")
DataFrame({
    'frac weights +ve': np.mean(components.iloc[:, :K].values >= 0, axis=0),
    'sum weights': np.sum(components.iloc[:, :K].values, axis=0),
    'sum sqr weights': np.sum((components.iloc[:, :K].values)**2, axis=0),
    'sum abs weights': np.sum(np.abs(components.iloc[:, :K].values), axis=0),
    'corr avg ret':  [np.corrcoef(avg, proj[:, i])[0, 1] for i in range(K)],
    'cumulative expl ratio': np.cumsum(pca.explained_variance_ratio_[:K])},
          index=[f"PC{i+1}" for i in range(K)]).round(4)

Top 20 principal components

	frac weights +ve	sum weights	sum sqr weights	sum abs weights	corr avg ret	cumulative expl ratio
PC1	1.0000	6.8350	1.0	6.8350	0.9988	0.5590
PC2	0.2449	0.0942	1.0	4.1476	0.0046	0.6218
PC3	0.5306	0.3638	1.0	3.5694	0.0142	0.6620
PC4	0.6735	0.9018	1.0	5.1037	0.0341	0.6994
PC5	0.4694	0.5504	1.0	5.2080	0.0185	0.7290
PC6	0.5510	0.7125	1.0	5.5172	0.0207	0.7510
PC7	0.5714	0.0807	1.0	5.5623	0.0021	0.7689
PC8	0.5510	0.0678	1.0	4.9024	0.0016	0.7831
PC9	0.5102	0.1727	1.0	5.1930	0.0040	0.7971
PC10	0.4898	0.2090	1.0	4.8891	0.0045	0.8091
PC11	0.4490	0.2954	1.0	5.0131	0.0063	0.8210
PC12	0.5306	0.0517	1.0	5.2657	0.0011	0.8321
PC13	0.6531	0.1003	1.0	4.8573	0.0020	0.8423
PC14	0.5102	0.1026	1.0	4.8301	0.0020	0.8521
PC15	0.4898	0.1416	1.0	4.8642	0.0027	0.8615
PC16	0.5102	0.0216	1.0	5.1350	0.0004	0.8703
PC17	0.4898	0.0855	1.0	5.3457	0.0015	0.8788
PC18	0.5714	0.1669	1.0	5.1840	0.0028	0.8864
PC19	0.5102	0.1752	1.0	5.1187	0.0029	0.8936
PC20	0.4694	0.1086	1.0	5.1526	0.0018	0.9007

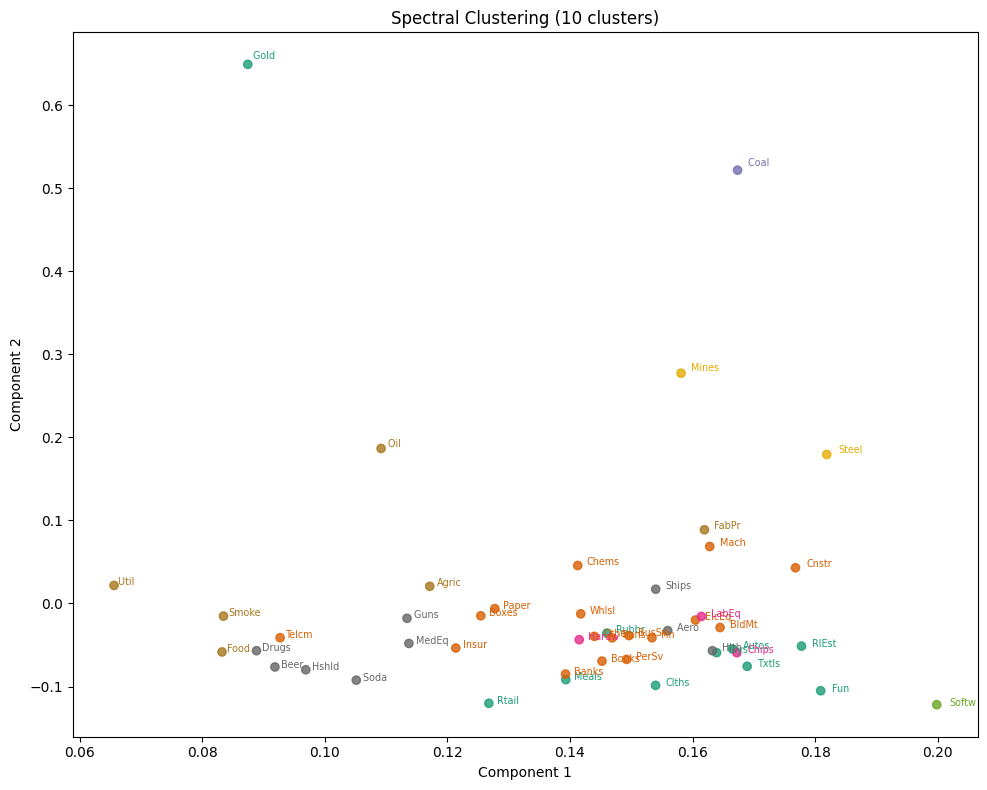
Spectral Clustering

Spectral clustering is a technique that groups data points based on the eigenvalues and eigenvectors of a similarity matrix. From the results, Component 1 primarily appears to capture market-wide beta risk sensitivity. Component 2 appears to reflect exposure to commodity-related factors (e.g. gold, coal and mining)

# Spectral clustering
spectral = cluster.SpectralClustering(
    n_clusters=10,
    eigen_solver="arpack",
    #affinity="nearest_neighbors",
    random_state=42,
)
spectral.fit(X.T)   # number of features equals the number observations dates
cmap = ColorMap(spectral.n_clusters, colormap='Dark2')
fig, ax = plt.subplots(figsize=(10, 8))
ax.scatter(components.iloc[:, 0], components.iloc[:, 1],
           c=cmap[spectral.labels_], alpha=.8)
for t, c, xy in zip(components.index, spectral.labels_,
                    components.iloc[:, :2].values):
    ax.annotate(text=t, xy=xy, xytext=xy * 1.01, color=cmap[c], fontsize='x-small')
ax.set_xlabel('Component 1')
ax.set_ylabel('Component 2')
ax.set_title(f"Spectral Clustering ({spectral.n_clusters} clusters)")
plt.tight_layout()
plt.show()

DataFrame({'cluster': spectral.labels_}, index=components.index).sort_values('cluster')

	cluster
Fun	0
Toys	0
Txtls	0
Clths	0
Rubbr	0
Autos	0
RlEst	0
Rtail	0
Meals	0
Gold	1
BldMt	2
ElcEq	2
Books	2
Telcm	2
Cnstr	2
Chems	2
Boxes	2
Paper	2
BusSv	2
Other	2
Fin	2
Insur	2
Banks	2
Trans	2
PerSv	2
Mach	2
Whlsl	2
Coal	3
Chips	4
LabEq	4
Hardw	4
Softw	5
Steel	6
Mines	6
Smoke	7
Food	7
FabPr	7
Oil	7
Agric	7
Util	7
Aero	8
Ships	8
Guns	8
Hlth	9
Hshld	9
Drugs	9
Soda	9
Beer	9
MedEq	9

EWMA

The Exponentially-Weighted Moving Average (EWMA) method assigns greater importance to recent data when estimating the covariance matrix, which is particularly useful for tracking market risk changes. JP Morgan RiskMetrics (1996) proposed a decay parameter \( \lambda = 0.97 \), implying a monthly decay rate of 0.03. The half-life of the weighting function represents the time required for a weight to decrease by 50%.

# Compute half-life of risk metrics' lambda for monthly data
def halflife(decay, half=0.5):
    """Returns halflife (t) from its definition: 0.5 = (1-decay)^t"""
    return -np.log(1/half)/np.log(1 - decay)

risk_metrics_lambda = 0.97   # for monthly data
print('Half-life: ', halflife(decay=1-risk_metrics_lambda).round(1), 'months')

Half-life:  22.8 months

def ewma(X, decay):
    """Helper to compute EWMA covariance matrix estimate"""
    weights = (1 - decay)**np.arange(len(X))[::-1]
    return (weights.reshape((1, -1)) * X.T) @ X / weights.sum()

Shrinkage methods

Covariance matrix estimates can be regularized using shrinkage. Ledoit and Wolf (1993) proposed shrinking the sample covariance matrix towards an identity matrix, and derived a closed-form formula to compute the asymptotically optimal shrinkage parameter \(\beta\) by minimizing a MSE criterion:

\[ (1 - \beta) \Sigma + \beta \dfrac{tr(\Sigma)}{N} I_n \]

Chen et al. (2010) proposed the Oracle Approximating Shrinkage (OAS) Estimator whose convergence is significantly better under the assumption that the data are Gaussian.

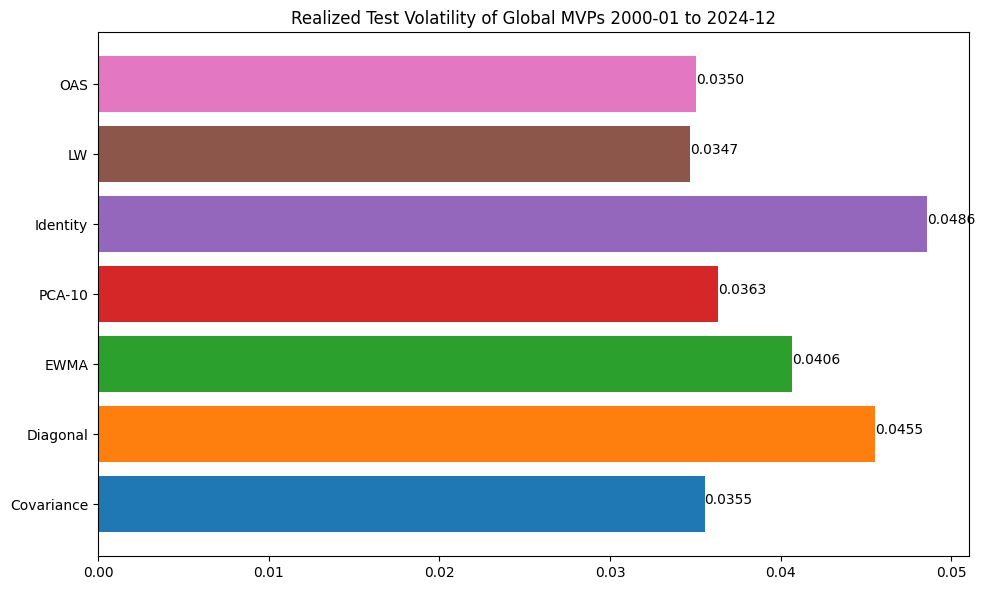
Volatility of the GMV portfolio

The out-of-sample (OOS) realized volatility of the Global Minimum Variance Portfolio (GMV) serves as a benchmark for evaluating covariance estimation accuracy. The GMV portfolio is designed to minimize total portfolio volatility. Since it relies on accurate covariance estimates, errors can lead to suboptimal diversification and higher realized volatility.

Beginning in January 2000, we update the covariance matrix estimate monthly using a rolling 30-year data window, and track the month-ahead return of the GMV portfolio. By the end of the test period, we expect the most accurate covariance matrix estimator to achieve the lowest return volatility.

# Helper method to compute Minimum Variance Portfolio and realized volatility
def gmv(cov, ret):
    """Compute minimum variance portfolio and return"""
    w = np.linalg.inv(cov) @ np.ones((cov.shape[1], 1))
    return float((np.array(ret) @ w/sum(w)).flatten()[0])

# Rolling monthly evaluation
decay = 0.03      # risk metrics monthly decay rate for EWMA
n_components = 10  # for PCA
split = '2000-01' # start rolling OOS prediction tests from this date

r = {}     # collect realized returns
for date in tqdm(rets.index[rets.index >= split]):
    X_train = rets.iloc[rets.index < date, :][-30*12:]   # 30 years of training data 
    X_test = rets.iloc[rets.index == date, :]      # predict one month ahead returns
    r[date] = {}

    # Empirical covariance
    cov = EmpiricalCovariance().fit(X_train).covariance_
    r[date]['Covariance'] = gmv(cov, X_test)
    r[date]['Diagonal'] = gmv(np.diag(np.diag(cov)), X_test)
    r[date]['EWMA'] = gmv(ewma(X_train, decay=decay), X_test)
    r[date][f"PCA-{n_components}"] = gmv(PCA(n_components).fit(X_train).get_covariance(), X_test)
    r[date]['Identity'] = gmv(np.identity(len(cov)), X_test)    
    r[date]['LW'] = gmv(LedoitWolf().fit(X_train).covariance_, X_test)
    r[date]['OAS'] = gmv(OAS().fit(X_train).covariance_, X_test)

100%|██████████| 300/300 [01:01<00:00,  4.86it/s]

ts = DataFrame.from_dict(r, orient='index')
vol = ts.std().rename('realized volatility').to_frame()
print('Realized volatility of minimum variance portfolio')
vol.T

Realized volatility of minimum variance portfolio

	Covariance	Diagonal	EWMA	PCA-10	Identity	LW	OAS
realized volatility	0.035531	0.045541	0.040645	0.036339	0.048569	0.034681	0.035041

Plot evaluation period realized volatility of minimum variance portfolios

fig, ax = plt.subplots(figsize=(10, 6))
values = vol.values.flatten()
ax.barh(vol.index, width=values, color=list(mcolors.TABLEAU_COLORS.values()))
for row, val in enumerate(values):
    ax.annotate(f"{val:.4f}", xy=(val, row))
ax.set_title(f"Realized Test Volatility of Global MVPs {split} to {rets.index[-1]}")
plt.tight_layout()